Statistics | The Bootstrap

Posted on:January 10, 2025

Table of contents

1. Understanding Bootstrap: The Motivation

Bootstrap is a powerful statistical tool used to quantify the uncertainty associated with a given statistic or estimator, such as the standard error or confidence interval.

Given that the population distribution is known, we can obtain the sampling distribution of a statistic/estimator by repeating the process of simulating N observations from the population K times, resulting in K realizations that approximate the sampling distribution.

However, in real-world scenarios, the population distribution is unknown. As a result, we cannot generate new samples from the original population. In such cases, we can sometimes rely on specific theorems that provide the sampling distributions for certain statistics or estimators, such as Central limited Theorem (CLT).

Even if we do not know the relevant theorem that indicates the sampling distribution, we can use simulation to approximate it >>> The bootstrap!

2. Parametric Bootstrap: Not That Important

This approach assumes the population follows a specified parametric distribution.

3. Non-parametric Bootstrap: It Is Important

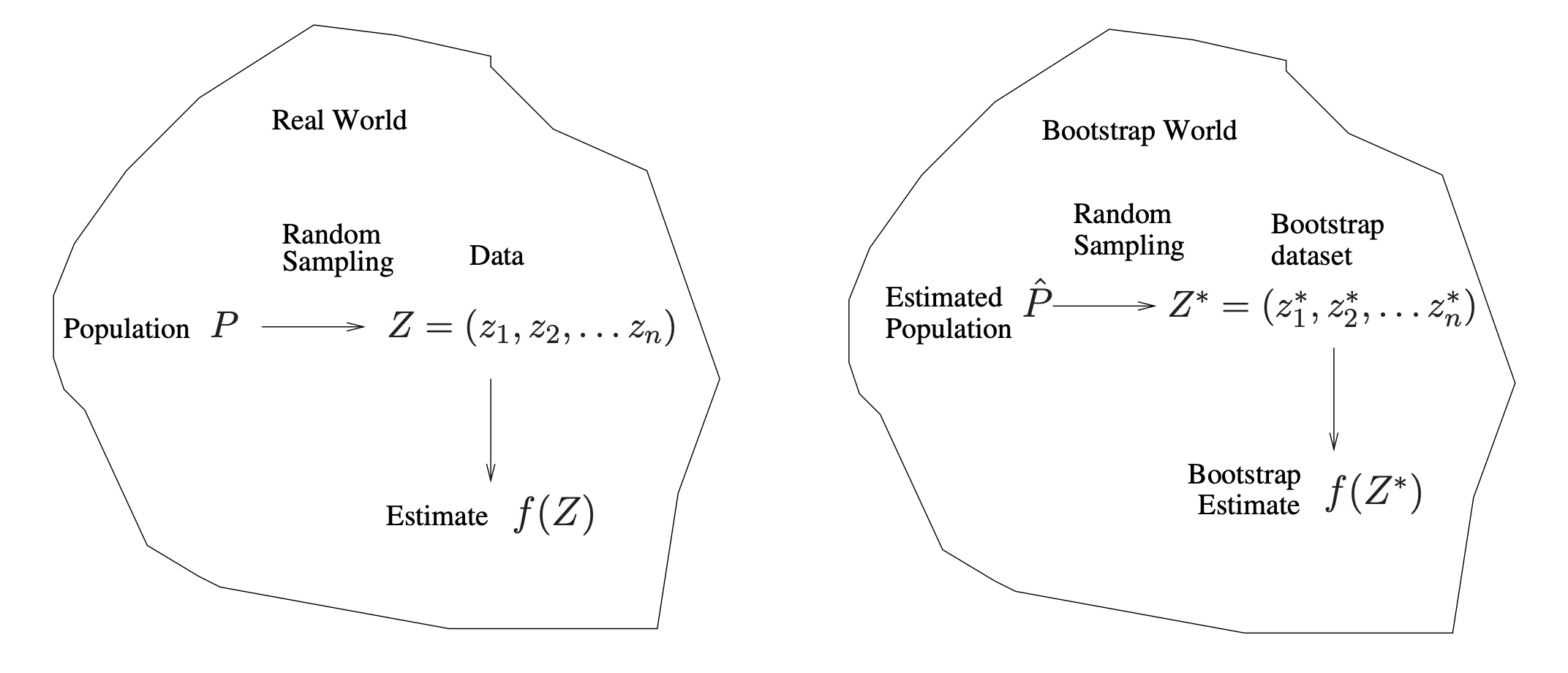
When we talk about “bootstrap,” we are usually referring to the non-parametric bootstrap. This is because the parametric bootstrap essentially involves repeatedly generating independent datasets from the (assumed) population. In contrast, the non-parametric bootstrap involves creating distinct datasets by repeatedly sampling the same number of observations from the original dataset with replacement.

In more complex data situations, it is crucial to determine the appropriate method for generating bootstrap samples. Generally, when setting up the bootstrap and organizing the sampling process, you must identify which parts of the data are independent.

In addition to obtaining standard errors for an estimator, the bootstrap method also provides approximate confidence intervals for a population parameter, which called the Bootstrap Percentile Confidence Interval.

4. Applications: Regression Coefficients

4.1. Three Approaches

To derive the sampling distribution of the estimator β^\hat{\beta} in regression, we can use several bootstrap approaches:

  1. Empirical Bootstrap: Also known as the “paired bootstrap,” this method treats (Xi,Yi)(X_i,Y_i) as one object. We then sample with replacement n times from these n objects to create a new bootstrap sample. For each bootstrap sample, we fit a linear regression.
  2. Residual Bootstrap: In this approach, we bootstrap the residuals and then regenerate Y. Using the bootstrap sample, we fit a linear regression as usual. We will delve into more detail about this process later.
    • Yi∗=β^0+β^1Xi+ϵ^i∗Y_i^* = \hat{\beta}_0 + \hat{\beta}_1 X_i + \hat{\epsilon}_i^* where ϵ^i∗∼(e1,e2,⋯ )\hat{\epsilon}_i^* \sim (e_1,e_2,\cdots)
  3. Wild Bootstrap: The Wild Bootstrap is similar to the residual bootstrap, but it differs slightly in the way Y is regenerated.
    • Yi∗=β^0+β^1Xi+VieiY_i^* = \hat{\beta}_0 + \hat{\beta}_1 X_i + V_i e_i where Vi∼N(0,1)V_i \sim N(0,1)
    • For the i-th observation, the wild bootstrap uses only its own residual. In contrast, the residual bootstrap probably use the residuals from other observations.

4.2. Residual Bootstrap

God’s perspective (known distribution and parameter):

  1. Generate ϵ\epsilon from a known distribution.
  2. Form y=Xβ+ϵ\mathbf{y} = X\beta+\epsilon for fixed XX and known β\beta.
  3. Compute β^\hat{\beta}.
  4. Repeat steps 1~3 many times.
  5. Estimate the sampling distribution of the estimated coefficients by the empirical distribution of the estimated coefficients from the simulated data sets.

Bootstrap’s perspective (unknown distribution and parameter):

  1. Generate ϵ∗\epsilon^* by sampling with replacement from ϵ^\hat{\epsilon}.
    • i.e., resample the residuals, whose mean is exactly 0.
  2. Regenerate y∗=Xβ^+ϵ∗\mathbf{y}^* = X \hat{\beta} + \epsilon^* for fixed X and known β^\hat{\beta}.
  3. Compute β^∗\hat{\beta}^* from (X,y∗)(X, \mathbf{y}^*).
    • i.e., bootstrap estimator β^∗=(XTX)−1XTy∗\hat{\beta}^* = (X^TX)^{-1}X^T \mathbf{y}^*.
  4. Repeat steps 1~3 many times.
  5. Estimate the sampling distribution of the estimated coefficients using the bootstrap distribution of the estimated coefficients from the bootstrapped data sets.

5. References