Statistics | Multilevel Modeling: A Non-Mathematical Revisit

Posted on:October 27, 2025

The most basic question about multilevel modeling: When and why should we use it?

First and foremost, the data must have a multilevel (or hierarchical) structure. Here are three examples (see following figures). However, almost all data can be conceptualized as multilevel to some extent. For instance, in social surveys, respondents are typically classified into two gender groups—male and female—and each individual belongs to one of these groups. Thus, “multilevel regression deserves to be the default form of regression” (McElreath, 2020, p. 15). For convenience, we refer to Level 1 as the individual level and Level 2 as the group level.

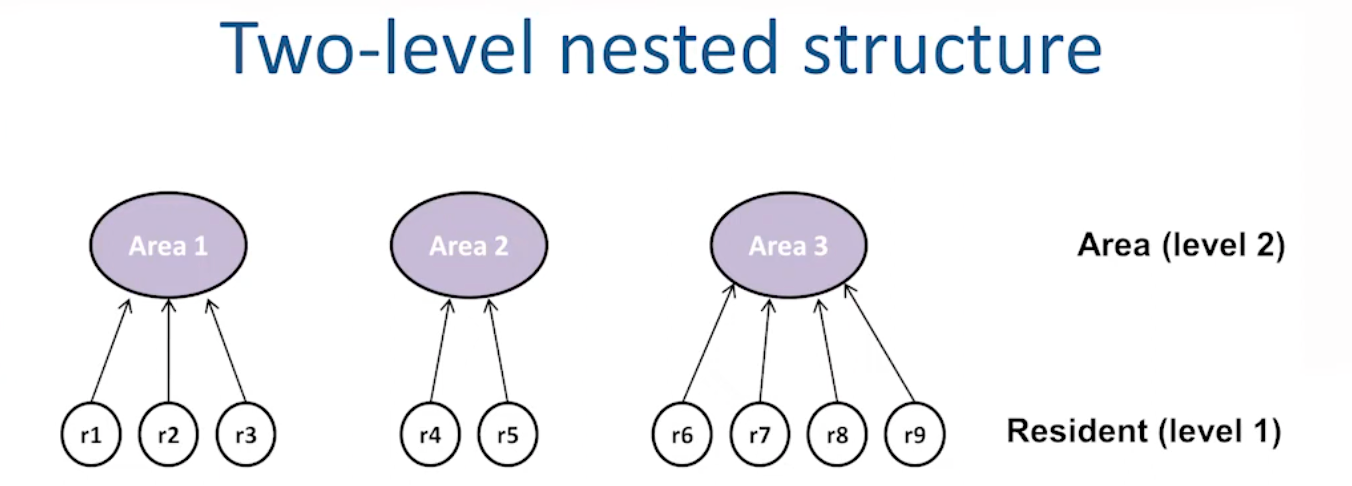
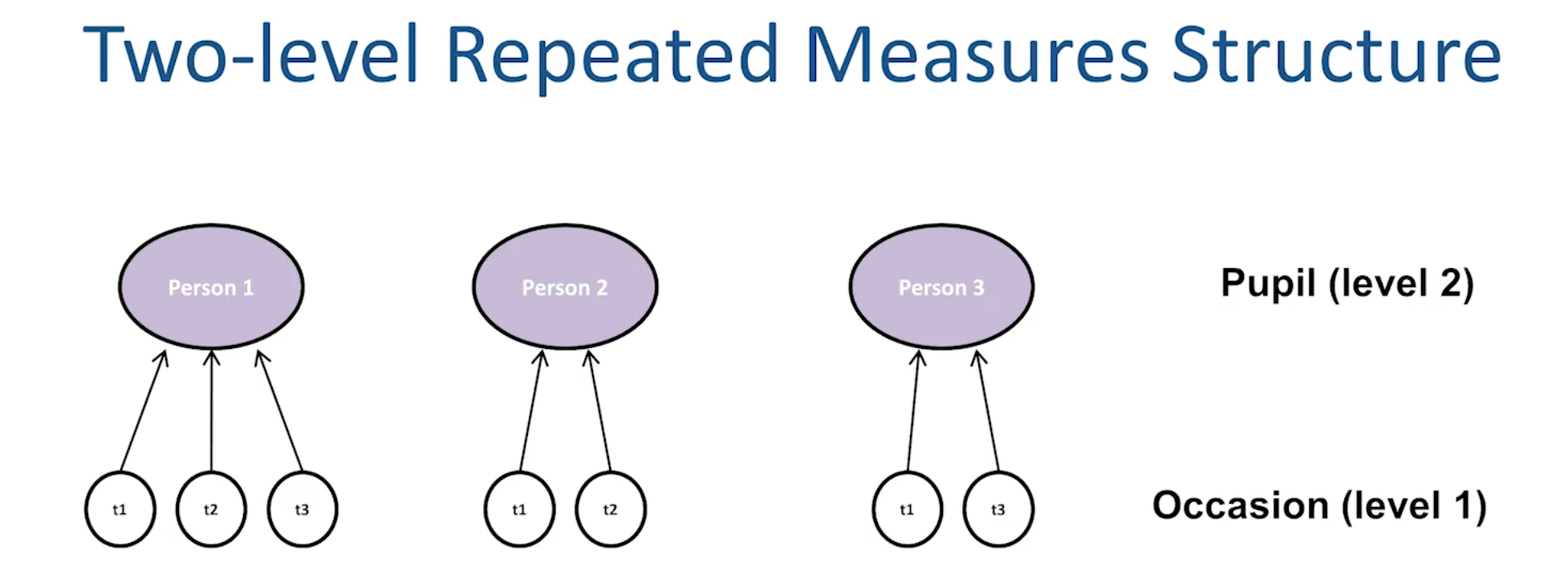
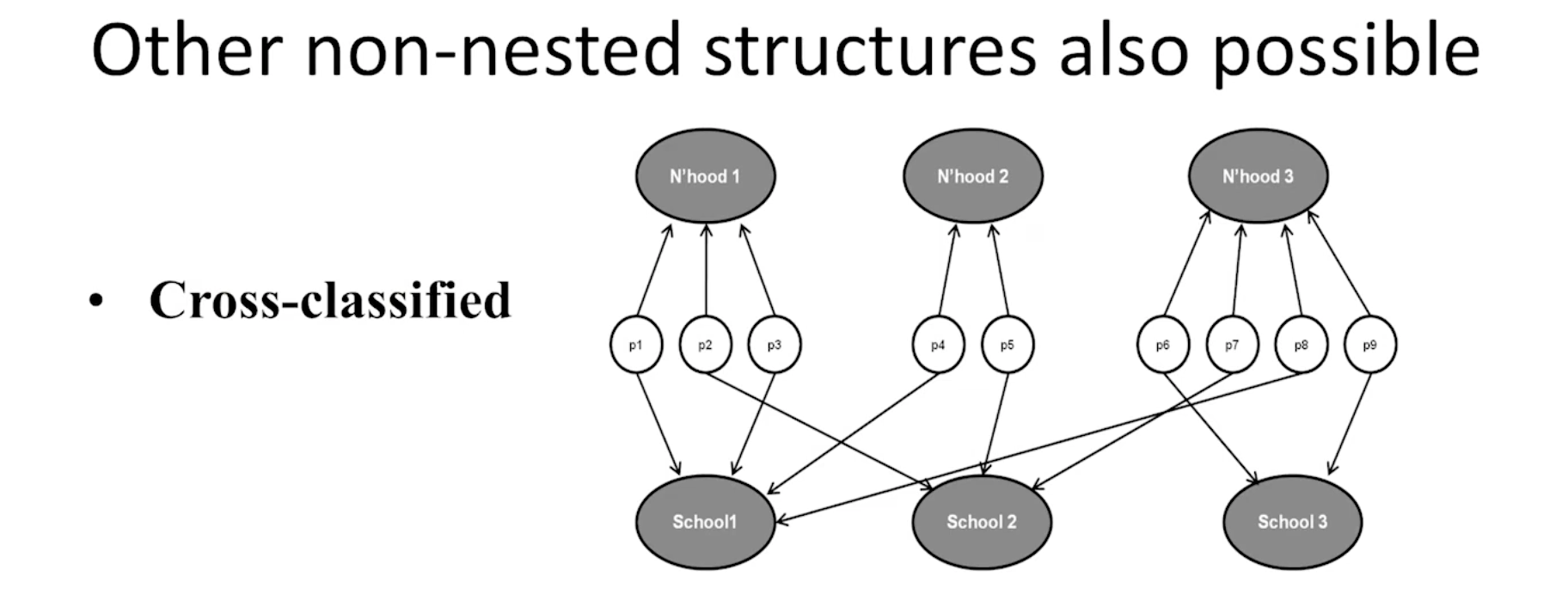
Second, one should believe that group-level information is useful for explaining individual level outcomes. There are two nuanced situations in which this applies:

  1. You explicitly hypothesize that groups can explain individual outcomes.
  2. You suspect that effects estimated solely from individual-level regressors are biased or misleading (as shown in the following figure).

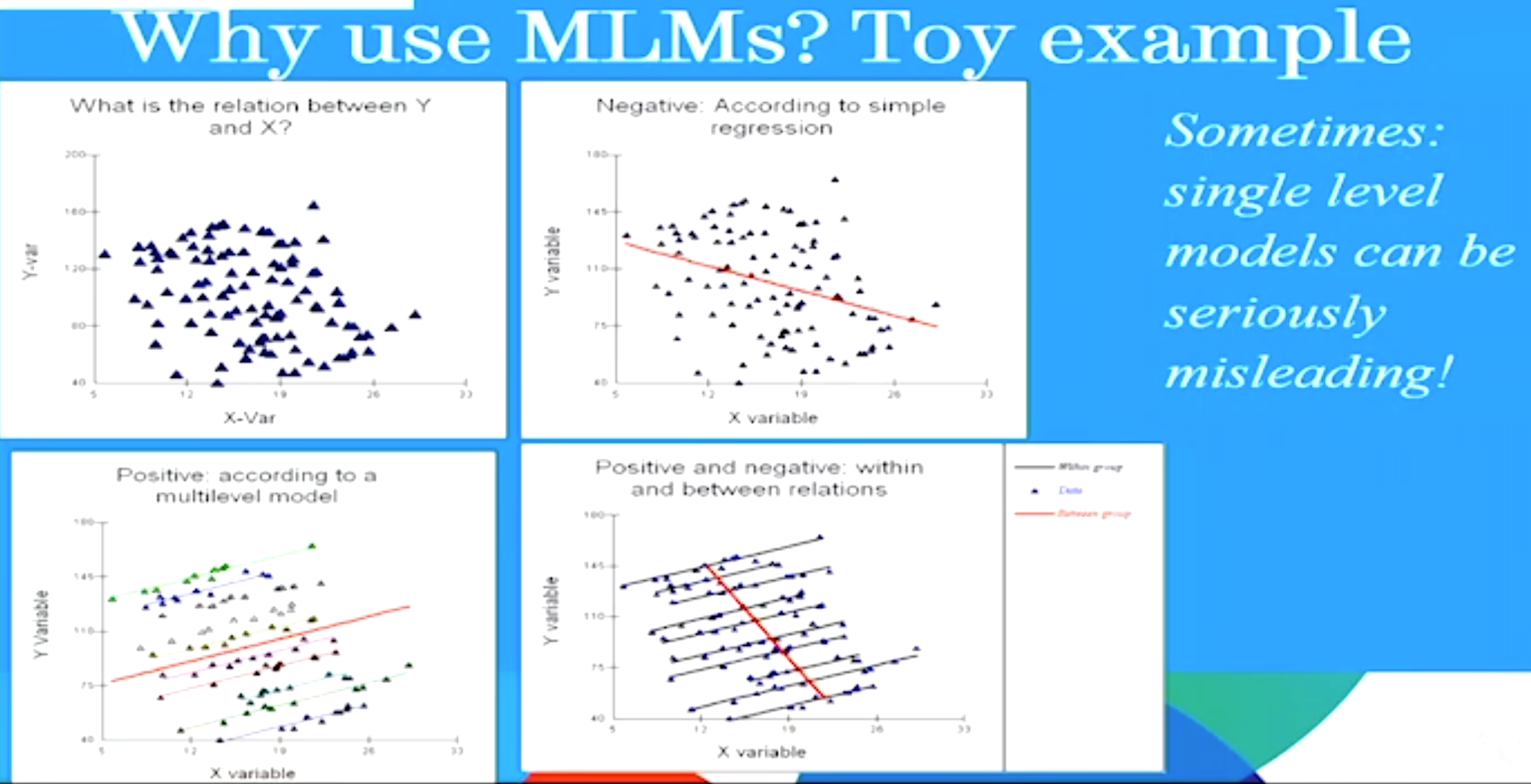
In such cases, a natural idea is to include group indicators as regressors in the model (i.e., control for groups), thereby incorporating group information into the explanation of individual-level outcomes. This approach is appropriate under two conditions:

  1. Methodological – when the number of groups is small (e.g., gender has only two categories), so the number of parameters remains manageable;
  2. Theoretical – when the groups in your dataset represent the entire population rather than a random sample. For example, there are only two genders in the world, but the number of schools far exceeds those included in your sample.

When neither of these conditions holds, it is natural to assume that there exists an underlying population of groups, and that the groups in your data are random samples drawn from this population. In that case, group-level effects are not independent but are assumed to arise from a common population distribution. This shared population enables partial pooling across groups—meaning that data from one group can inform estimates for another. This is fundamentally different from adding group dummies directly into a regression model (the no pooling approach), which treats all groups as completely independent.

References