Statistics | One-sided or Two-sided Test?

We should determine whether to use a one-sided test or a two-sided test based on the problem specification (i.e. 问题的提法). More specifically, it should be determined based on the form of the alternative hypothesis (i.e. 备择假设的形式).

若我们知道待检参数在违背零假设H0的情况下会朝哪边偏离，就使用单侧检验；如果不知道，那么就使用双侧检验——这可以通过观察备择假设H1的设定形式判断出来。下面我们以单样本正态均值检验为例。

双侧检验 (Two-sided test)

假设总体服从均值为μ、方差为σ2的正态分布，其中方差已知。我们的假设设定为：

H_0: \mu = \mu_0\\ H_1: \mu \ne \mu_0

这样设定H1，是因为我们并不知道如果μ不等于μ0，它会往哪边偏离。若H0成立，则样本均值 $\bar{X}$ 作为总体均值μ的无偏点估计，应该“接近”μ0。因此我们的检验设定为：

if\ |\bar{X} - \mu_0| > d,\ reject\ H_0

并设定我们的显著性水平为α，即该检验犯第一类错误（i.e. 在H0为真的条件下，拒绝H0）的概率不能高于α。常见的α为0.05。因此：

P(|\bar{X} - \mu_0| > d\ |\ H_0\ is\ true ) \le \alpha

注意到H0成立时， $(\bar{X}-\mu_0)/(\sigma/\sqrt{n}) \sim N(0,1)$ 。再根据：

Prob(|\frac{\bar{X} - \mu_0}{\sigma/\sqrt{n}}| > \frac{d}{{\sigma/\sqrt{n}}}) \le \alpha

可以求得：

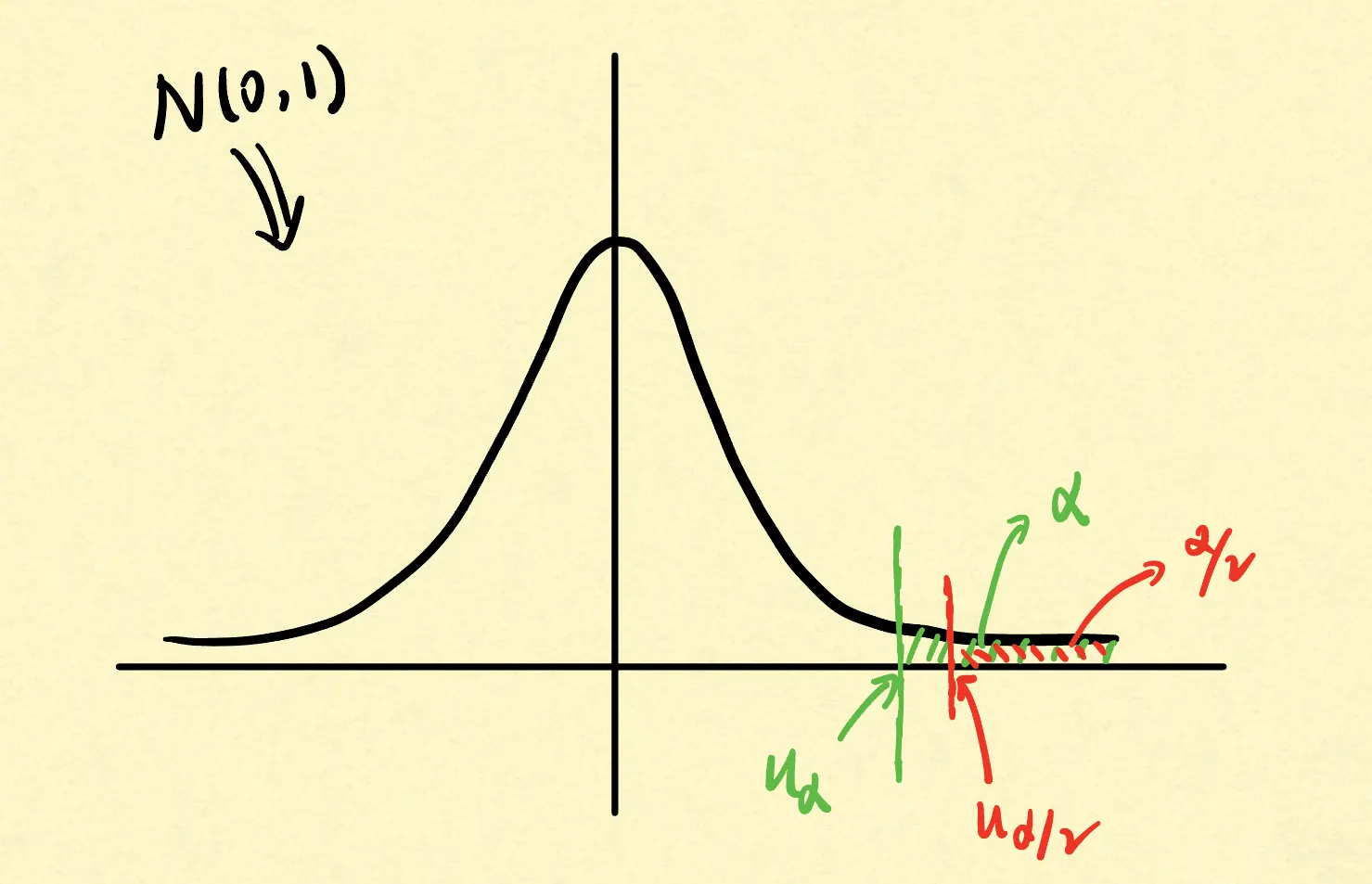
d = \frac{\sigma}{\sqrt{n}}u_{\alpha/2}

其中u为标准正态分布的上分位数。综上，该假设的检验为：当 $|\bar{X} - \mu_0| > \frac{\sigma}{\sqrt{n}}u_{\alpha/2}$ 时，拒绝H0。

单侧检验 (One-sided test)

若我们已经知道如果μ不等于μ0，必有μ大于μ0，那么我们的假设设定变为：

H_0: \mu = \mu_0\\ H_1: \mu > \mu_0

同样，若H0成立，则样本均值 $\bar{X}$ 作为总体均值μ的无偏点估计，应该“接近”μ0，但会是从右侧接近。因此我们的检验设定为：

if\ \bar{X} - \mu_0 > d,\ reject\ H_0

设定显著性水平为α。因此：

P(\bar{X} - \mu_0 > d\ |\ H_0\ is\ true ) \le \alpha

通过类似的推导，我们可以计算出：

d = \frac{\sigma}{\sqrt{n}}u_{\alpha}

综上，该假设的检验为：当 $\bar{X} - \mu_0 > \frac{\sigma}{\sqrt{n}}u_{\alpha}$ 时，拒绝H0。