Statistics | Poisson Model

Posted on:January 16, 2025

Table of contents

1. The Basic

The pmf of a Poisson random variable X∼Poi(λ)X \sim \text{Poi}(\lambda ):

P(X=k)=e−λλk/k!(k=0,1,2,⋯ )P(X=k) = e^{-\lambda} \lambda^k /k!\quad (k=0,1,2,\cdots)

where λ>0\lambda > 0 called the “rate” parameter. This pmf can be easily verified as valid by using the fact that λkk!\frac{\lambda ^k}{k!} is the Taylor expansion of eλe^\lambda at 0. Also, we have:

E(X)=Var(X)=λE(X)= Var(X)=\lambda

2. Application

The Poisson distribution is often used to count the number of “successes” in scenarios involving a large number of trials, each with a small probability of success. For example,

“The Poisson Approximation”: Event A1,A2,⋯ ,AnA_1, A_2, \cdots, A_n with P(Aj)=pjP(A_j) = p_j, nn is large and pjp_j’s are all small; These events are independent or weakly dependent >>> Then, the number of events that occur is approximately a Poisson with λ=∑j=1npj\lambda = \sum_{j=1}^n p_j.

Let X∼B(n,p)X \sim B(n, p). As n→∞n \to \infty and p→0p \to 0 such that npnp remains constant (i.e., their rates of convergence are similar), the pmf of XX converges to the pmf of a Poisson distribution with parameter λ=np\lambda = np.

P(X=k)=(nk)pk(1−p)n−k=n(n−1)⋯(n−k+1)⋅λkk!nk(1−λn)n(1−λn)−k=λkk!lim⁡n→∞(1−λn)n=λkk!e−λ\begin{aligned} P(X=k) &= \binom{n}{k}p^k (1-p)^{n-k} \\ &= \frac{n(n-1)\cdots(n-k+1)·\lambda^k}{k! n^k} (1-\frac{\lambda}{n})^{n}(1-\frac{\lambda}{n})^{-k} \\ &= \frac{\lambda^k}{k!} \lim_{n \to \infin}(1-\frac{\lambda}{n})^{n} \\ &= \frac{\lambda^k}{k!} e^{-\lambda} \end{aligned}

Summary: Binominal can converge to a Poisson in a certain way.

4. Poisson Regression

Poisson regression should be used when DV is a count variable, such as the number of times an event occurs in a given time period. Model specification:

yi∼Poi(λi)ln⁡(λi)=βTxiy_i \sim \text{Poi}(\lambda_i)\\ \ln(\lambda_i) = \beta^T\mathbf{x}_i

5. Poisson Regression with Offset

Special case: when yiy_i’s represent the counts within the different time interval.

In this case, the data are like (xi,yi,ti)(x_i, y_i, t_i), instead of the original (xi,yi)(x_i, y_i). We can still use the Poisson model with a slight modification as follows:

yi∼Poi(λiti)ln⁡(λi)=βTxiy_i \sim \text{Poi}(\lambda_i t_i)\\ \ln(\lambda_i) = \beta^T\mathbf{x}_i

Here, λi\lambda_i represents the count per unit length of time and tit_i represents the number of time units. Then, we perform the following transformation:

yi∼Poi(λiti)ln⁡(λiti)=βTxi+ln⁡(ti)y_i \sim \text{Poi}(\lambda_i t_i)\\ \ln(\lambda_i t_i) = \beta^T\mathbf{x}_i + \ln(t_i)

Let λi′=λiti\lambda'_i = \lambda_it_i, and then we can treat it as a “standard Poisson regression + adjusted systematic linkage.” Here, ln⁡(ti)\ln(t_i) is referred to as the offset.

6. Example: Age-Grouped Cancer Incidence in Danish Cities

The eba1977 dataset from the ISwR package contains counts of incident lung cancer cases and population size in four neighbouring Danish cities by age group:

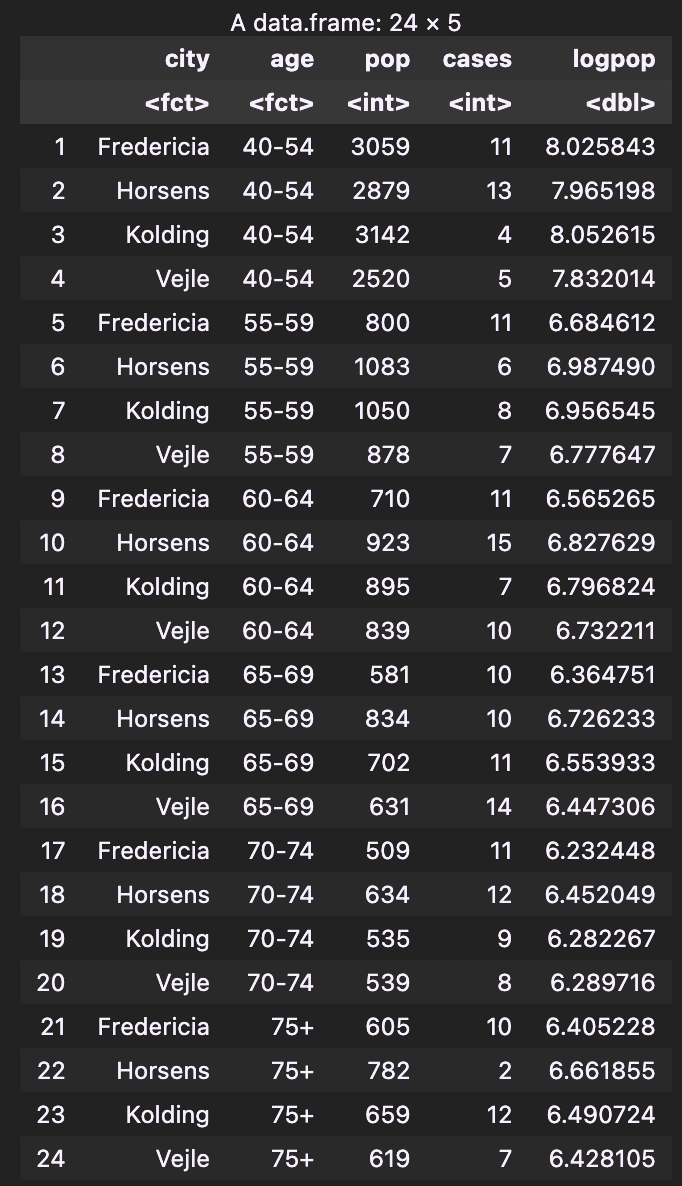
In this dataset, “pop” (i.e. population) is an attribute regarding to interval. Thus, we should use the Poisson model with offset. In this case, λi\lambda_i represents the “#cancer cases/per person”, which is exactly the probability of developing cancer.

## Import data
data(eba1977)
cancer.data = eba1977

## Add the offset column
logpop = log(cancer.data[ ,3])
new.cancer.data = cbind(cancer.data, logpop)

## GLM model
model = glm(cases ~ city + age+ offset(logpop),
            family = poisson(link = "log"), data = new.cancer.data)
summary(model)

The summary report:

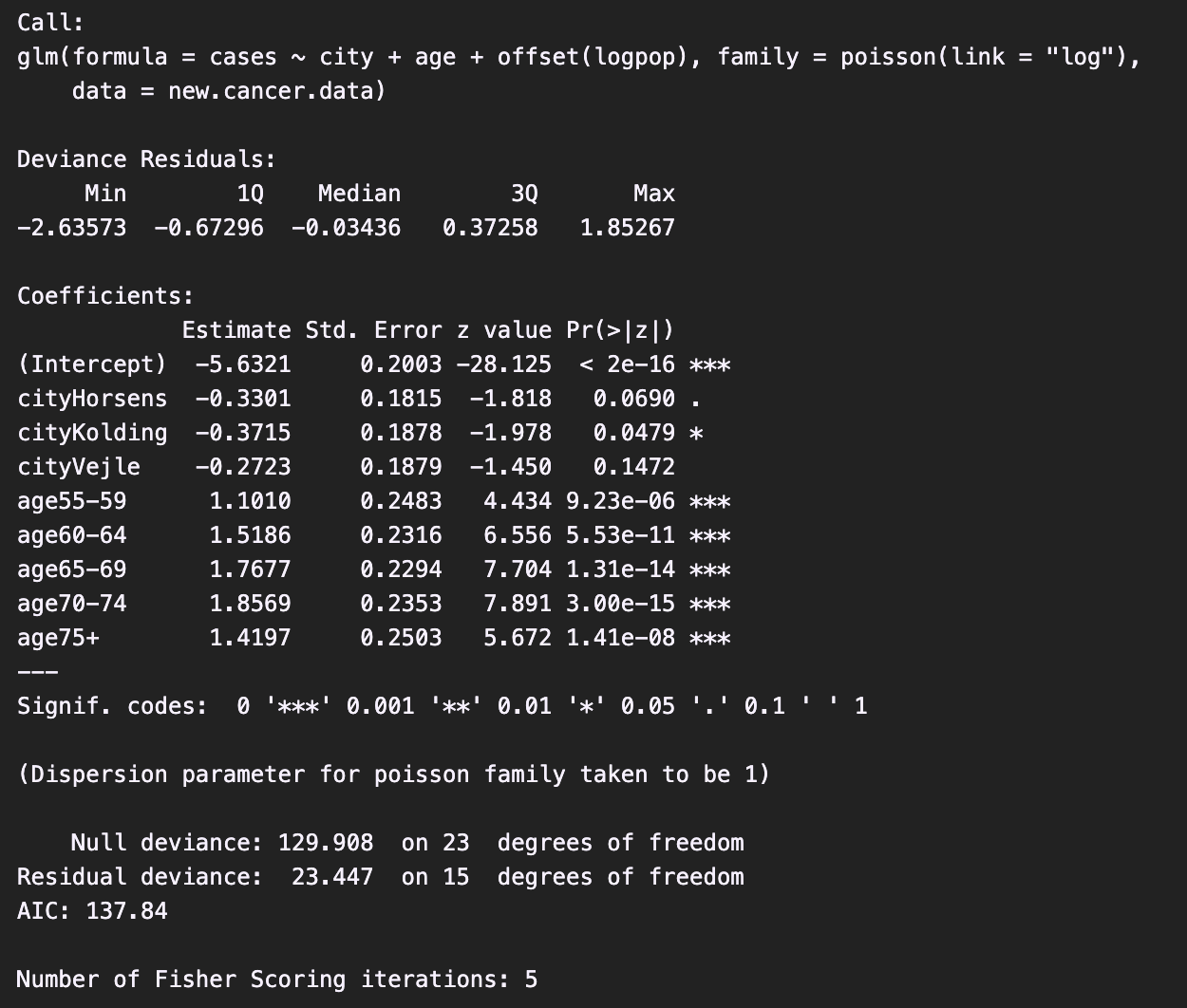
Interpretation of some coefficients:

7. References