Table of contents
- 1. Expression and Environment
- 2. Defining New Functions
- 3. Control Flow
- 4. Higher-Order Functions
- 5. Recursion
- Reference
1. Expression and Environment
1.1 Expressions
An expression describes a computation and evaluates to a value. 两种类型:
- primitive expression
- number: 如
2 - name: 如
add - string: 如
'hello'
- number: 如
- call expression
- 如
max(2,3)
- 如
Call Expressions
- 形为f(x)的expressions.
- All expressions can use function call notation.
- 不需要运算优先级——全凭nesting structure.
Evaluation Procedure for Call Expressions
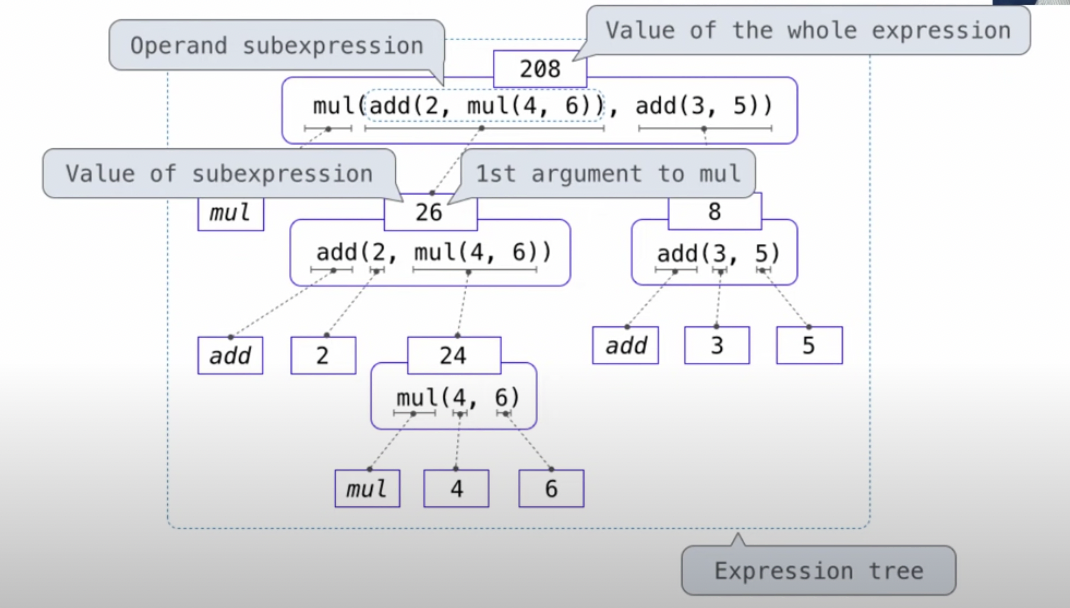
- Evaluate the operator and then the operand subexpressions(先操作符,再操作数).
- Apply the function that is the value of the operator subexpression to the arguments that are the values of the operand subexpression(操作符和操作数都要evaluate完才能进行计算).
1.2 Environment
Name and Assignment Statement
- 使用assignment statement 「=」,即「name = expression」,先evaluate右边的expression,然后bind它到左边的name上——这样value就有了name,可以反复使用。
- 除了「=」,还有2种绑定name和value的方法:①import语句 ②def语句
Environment

- Def: Environment diagrams visualize the interpreter’s process.
- It keeps track of bindings between names and values.
- 【一个environment由一串frames构成】An environment in which an expression is evaluated consists of a sequence of frames, depicted as boxes.
- 【每个frame由多个bindings构成】Each frame contains bindings, each of which associates a name with its corresponding value.
- 【只有一个global frame】There is a single global frame——目前我们也只遇到仅有global frame的场景.
Execution Rule for Assignment Statements
- Evaluate all expressions to the right of = from left to right(等号右边的从左到右依次eval).
- Bind all names to the left of = to the resulting values in the current frame(将等号左边的name和右边的value一一对应bind起来).
2. Defining New Functions
2.1 Define a Function
# 其中<name>(<formal parameters>)被称为“function signature(函数签名)”
def <name>(<formal parameters>):
return <return expression>def statement执行的规则:
- Create a function with signature
<name>(<formal parameters>) - Set the body of that function to be everything indented after the first line
- Bind
<name>to that function in the current frame

- An
importstatement binds a name to a built-in function. - A
defstatement binds a name to a user-defined function created by the definition. - Each function is a line that starts with
func, followed by the name and formal params. - The name appearing in the function is called the intrinsic name.
- The name in a frame is a bound name.
- Different names may refer to the same function, but that function itself has only one intrinsic name.
2.2 Call a User-Defined Function
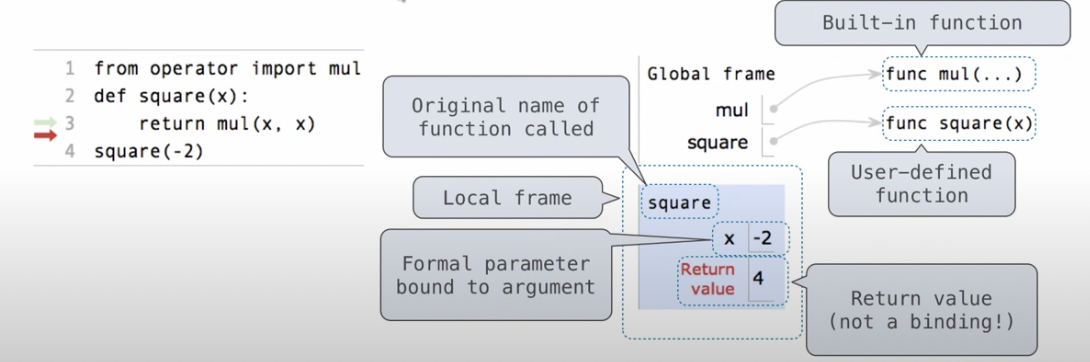
Execution Rule for Calling User-defined Functions
- Add a local frame, forming a new environment(local frame的名字一般就用函数的名字).
- Bind the function’s formal parameters to its argument values in that frame.
- Execute the body of the function in that new environment.
2.3 Non-pure Functions
「print sth.」 vs 「evaluate sth.」
- 打印None,会显示None;但evaluate None,不会显示None
- 如果一个function 不显示地返回一个值,它返回None
Noneis not displayed by the interpreter as the value of an expressionprint(print(1), print(2))
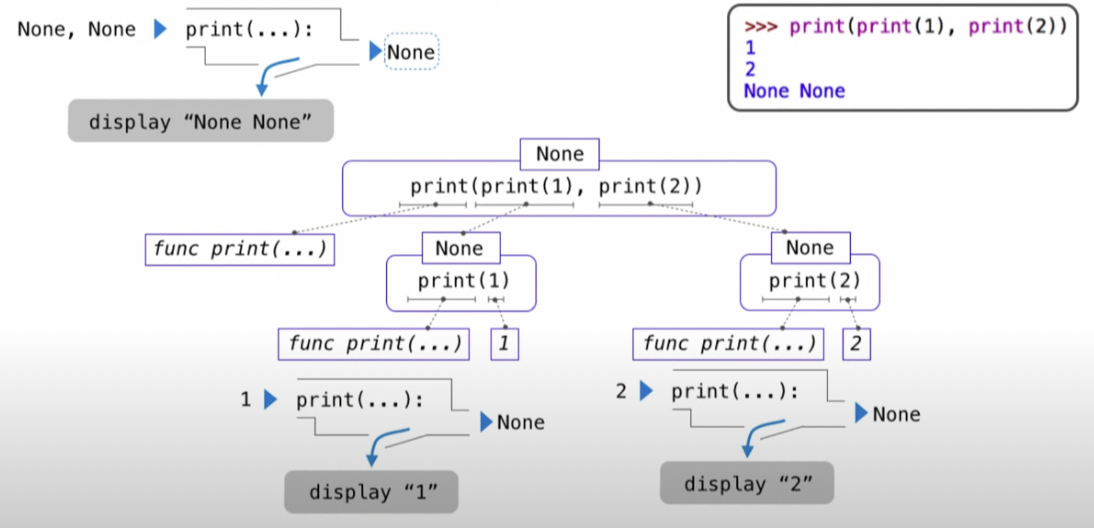
Pure function vs Non-pure function
- 前者仅仅只return values,不造成其他任何影响
- 后者会造成一些影响——side effects
2.4 Multiple Environment: An Example
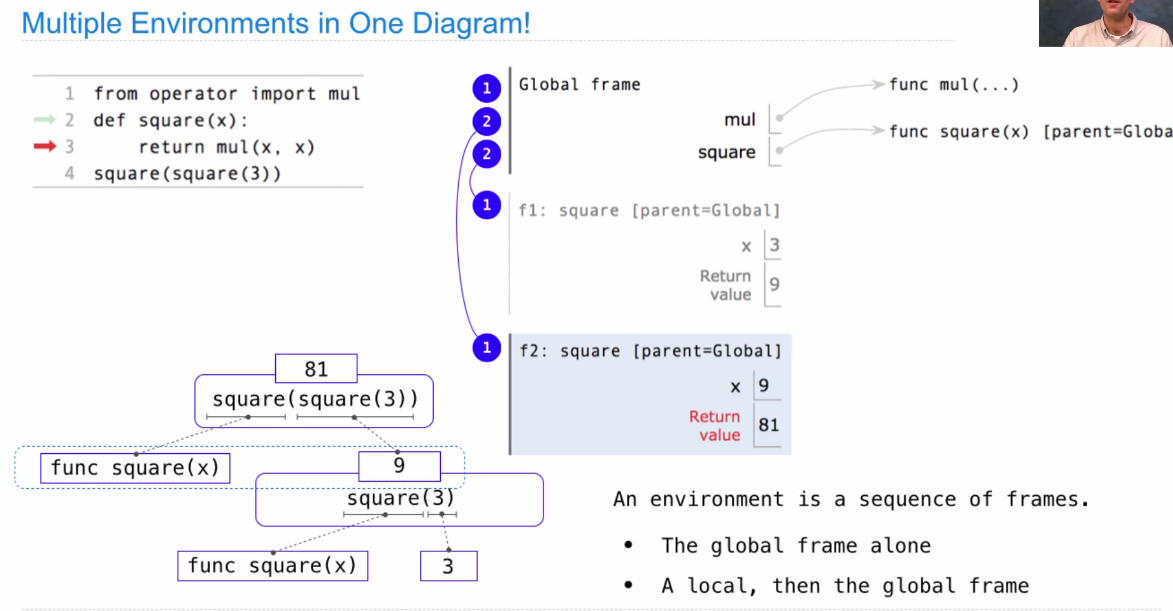
上图中有3个different environments:
- Global frame
- Global frame + f1 frame
- Global frame + f2 frame
Looking up names in environments
- An environment = a sequence of frames
- 一个name,在current environment中,最先找到bind的那个frame
Review: def statement执行的规则>>>画diagram
- 定位当前的frame
- 在该frame里写出function name
- 在该frame外创建function object
func <name>(<formal parameters>) [parent=当前frame]- 若是lambda函数,这里的
<name>写λ
- 箭头从frame里的function name指向frame外的function object
2.5 补充例子:同名函数
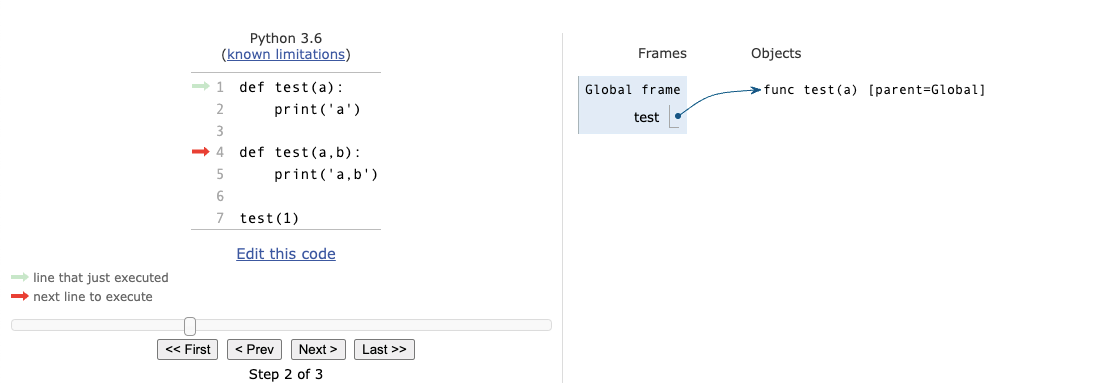
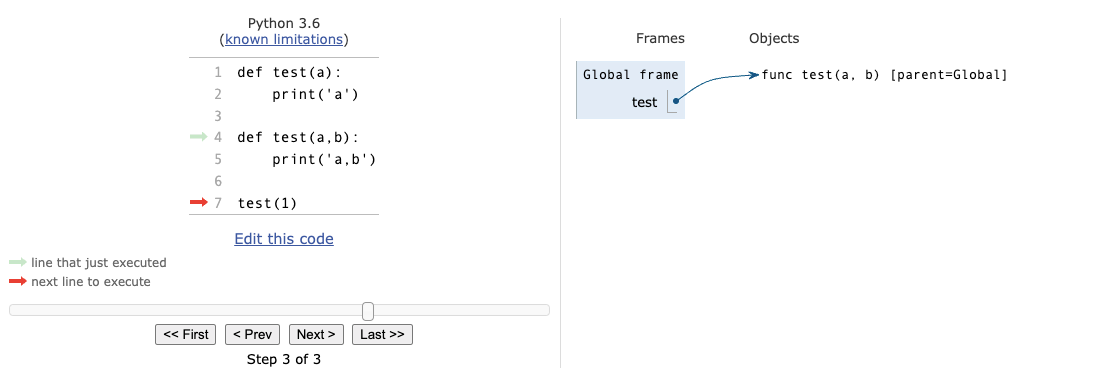
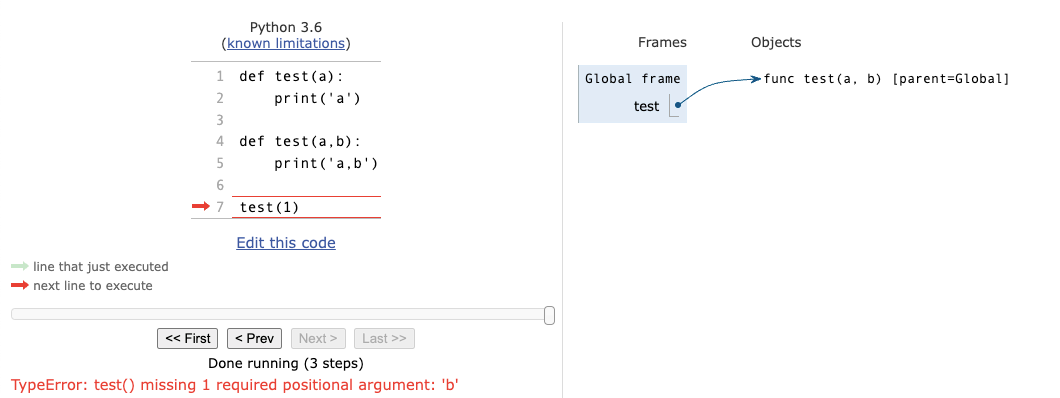
- 错误原因:执行完第二个def后,在global frame里,test这个name,已经和test(a,b)这个函数实体绑定了,而之前和test这个name绑定的test(a)这个函数实体已经没有了name与它绑定。此时再调用test这个函数并仅传一个参数,就会报错,因为它预期会有两个参数传进来。
3. Control Flow
3.1 Control Expressions
Logical operators
<left> and <right>的规则(注意”短路“):
- Evaluate the subexpression
<left>. - If the result is a false value
v, then the expression evaluates tov. - Otherwise, the expression evaluates to the value of the subexpression
<right>.
<left> or <right>的规则(同样”短路“):
- Evaluate the subexpression
<left>. - If the result is a true value
v, then the expression evaluates tov. - Otherwise, the expression evaluates to the value of the subexpression
<right>.
「短路规则」可以使得一些状况下不crash!
Conditional expression
<consequent> if <predicate> else <alternative>- Evaluation Rule:
- Evaluate the
<predicate>expression. - If it’s a true value, the value of the whole expression is the value of the
<consequent>. - Otherwise, the value of the whole expression is the value of the
<alternative>.
- Evaluate the
3.2 Conditional Statements
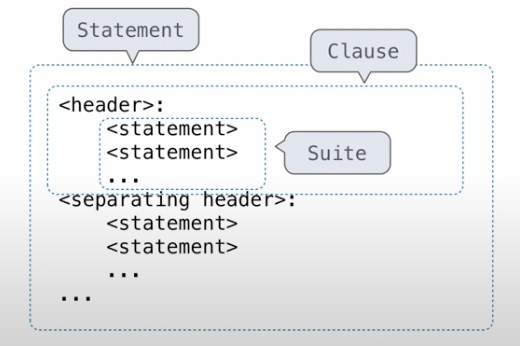
Statements
- A statement is executed by the interpreter to perform an action.
- Compound statements (嵌套) ↑↑↑
Conditional statements——If
- Always starts with
ifclause. - Zero or more
elifclauses. - Zero of one
elseclause, always at the end.
Boolean Contexts
- False values in Python:
False,0,'',None,[]
3.3 Iteration
「while」 statement
- Evaluate the header’s expression.
- If it is a true value, execute the (whole) suite, then return to step.
「for」 statement
- 暂无
3.4 Testing
“Testing a function” is the act of verifying that the function’s behavior matches expectations.
Test的思路:
- Contains one or more sample calls to the function being tested.
- The returned value is then verified against an expected result.
方法1:Assertions
- Expression in a boolean context + A quoted line of text.
- If the expression evaluates to a false value: Causes an error + Display the text.
- If the expression evaluates to a true value: No effect.
方法2:Doctests (Docstring)
- line 1: A one-line description of the function
- line 2: A blank line
- line 3+: A detailed description of arguments and behavior (optional)
- line 3++: a sample interactive session that calls the function,如↓↓↓
>>> def sum_naturals(n):
"""Return the sum of the first n natural numbers.
>>> sum_naturals(10)
55
>>> sum_naturals(100)
5050
"""
total, k = 0, 1
while k <= n:
total, k = total + k, k + 1
return totalWhen writing Python in files, all doctests in a file can be run by starting Python with the doctest command line option: python3 -m doctest <python_source_file>
4. Higher-Order Functions
What is a Higher-Order Functions? A function that takes a function as an argument value or returns a function as a return value. Some advantages:
- Express general methods of computation
- Remove repetition from programs
- Separate concerns among functions
4.1 Functions as Arguments
迭代法逼近黄金分割比:
- guess >>> 一开始瞎猜的数,但随着后来的更新,会逐渐逼近黄金分割
- update >>> 更新函数,按一定规则将guess更新为更接近目标值的数
- close >>> 判断guess和黄金分割是否足够近,以决定是否继续更新
def improve(update, close, guess=1):
while not close(guess):
guess = update(guess)
return guess以上的代码框架让我们先撇开细节,注重问题的解决逻辑。下面我们再具体实现update和close函数:
def golden_update(guess):
return 1/guess + 1
# check是否逼近x^2 - x - 1 = 0的根——黄金分割
def square_close_to_successor(guess):
return approx_eq(guess * guess, guess + 1)
# 判断两个数是否足够近
def approx_eq(x, y, tolerance=1e-15):
return abs(x - y) < tolerance
# >>> improve(golden_update, square_close_to_successor)
# 1.6180339887498951上面的例子反映了两件事:
- Naming and functions allow us to abstract away a vast amount of complexity.
- It is only by virtue of the fact that we have an extremely general evaluation procedure for the Python language that small components can be composed into complex processes.
4.2 Nested Definitions
在global frame里定义一堆函数的缺点:
- The global frame becomes cluttered with names of functions, which must all be unique.
- We are constrained by particular function signatures: the
updateargument toimprovemust take exactly one argument——如果某个update函数要吃两个参数,就会出问题。
因此,提出nested function definitions,解决上述两个问题。以「迭代法求平方根」为例:反复执行下面的sqrt_update函数,就会得到a的平方根。但与4.1中迭代法求黄金分割不同的是,这个update函数要求两个参数,而我们抽象出的improve函数只能接受参数数目为1的update函数。
def average(x, y):
return (x + y)/2
def sqrt_update(x, a):
return average(x, a/x)
# 回顾:抽象的improve函数
# def improve(update, close, guess=1):
# while not close(guess):
# guess = update(guess)
# return guess如何修改上述代码使其与improve函数兼容?使用nested functions:
def sqrt(a):
def sqrt_update(x):
return average(x, a/x)
def sqrt_close(x):
return approx_eq(x * x, a)
return improve(sqrt_update, sqrt_close)↑↑↑ local def statements only affect the current local frame >>> Locally Defined Functions: these local def statements don’t even get evaluated until sqrt is called!

- 每个user-defined function都有一个parent frame:就是该函数定义时所在的frame;
- 当该function被调用时会创建一个parent frame为该function的parent frame的local frame;
- 因此内嵌的函数have access to the names in the environment where they are defined (not where they are called).

↑↑↑ 以上图中的environment diagram为例:调用inner function sqrt_close的时候,它的local frame只能访问到它的上一级函数的local frame(f1)中的东西和global frame中的东西,而并不可以访问到调用它的函数的local frame(f2)中的东西。
因此优点为:The names of a local function do not interfere with names external to the function in which it is defined —— because the local function name will be bound in the current local environment in which it was defined, rather than the global environment.
小结:
- 一个function被def时:一定是在一个frame里被def的,该frame成为该function的parent。
- 一个function被call时:创建一个local frame,该local frame的parent是这个function的parent,也就是该function被定义时所在的frame,而非该function被调用时所在的frame。
4.3 Functions as Returned Values
Locally defined functions maintain their parent-frame environment when they are returned.
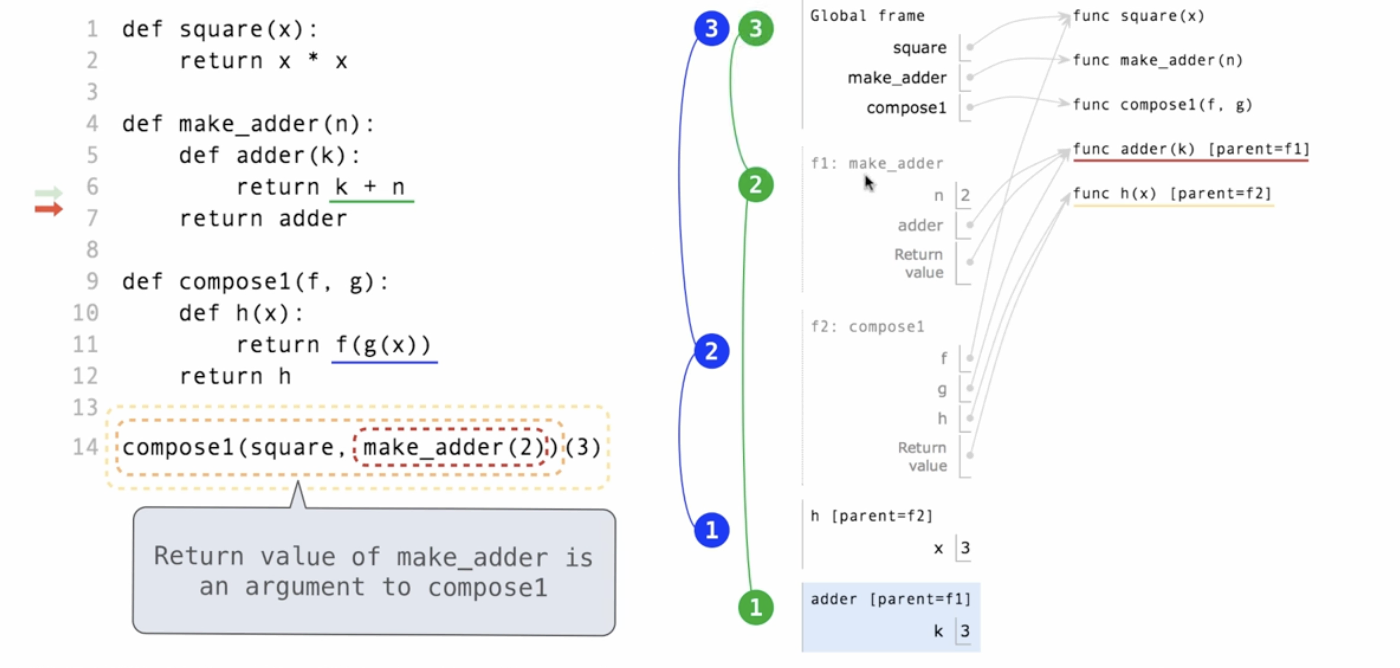
即使adder已经被return了,后面调用它的时候依然可以追溯到它的environment(f1已经灰了)。
Self-Reference:The function could refer to its own name within its body.
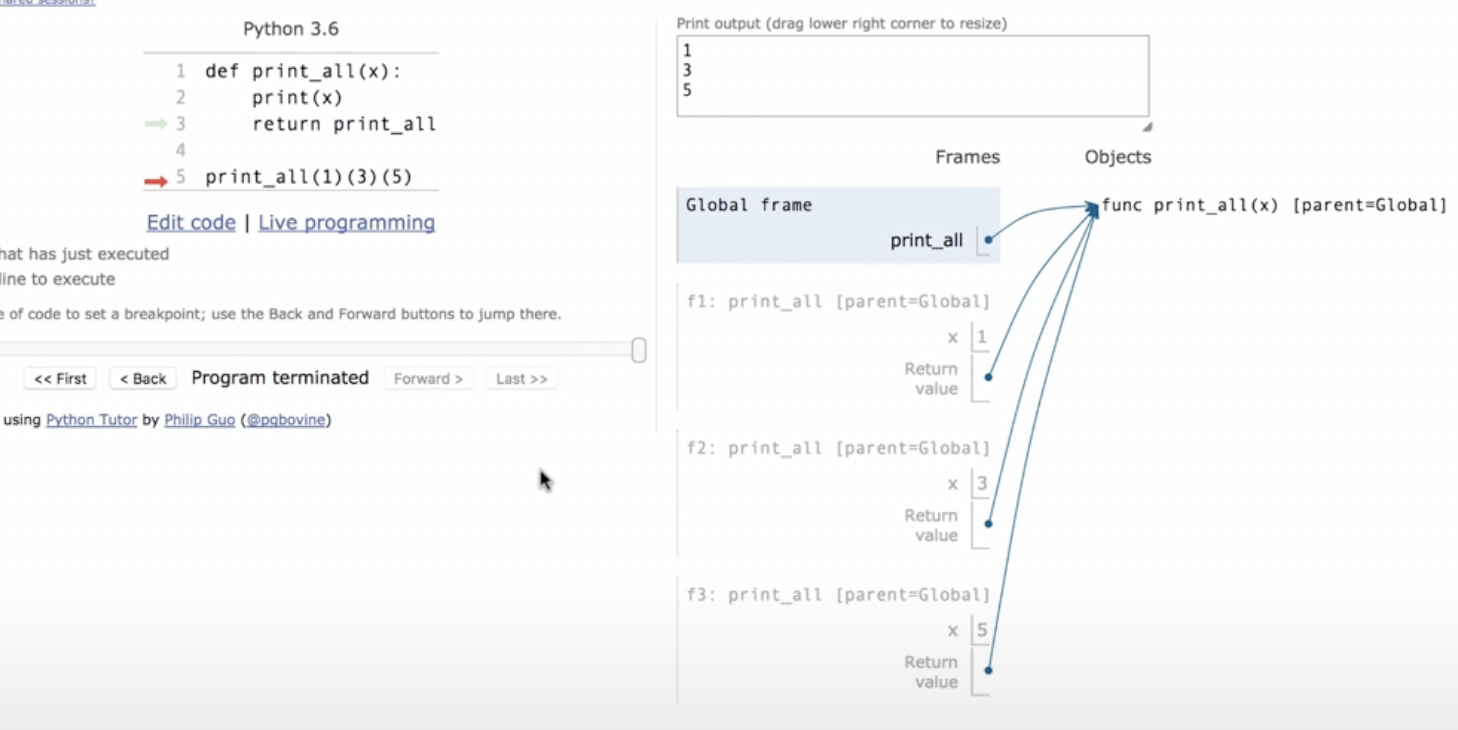
本质:在function内部可以访问到global frame中的names。
4.4 「Application 1」Currying
将一个「多参数函数」转换为一个等价的「单参数高阶函数」,即f(x,y)->g(x)(y)
Transforming a multi-argument function into a single-argument, higher-order function.
例如,下面的make_adder就是add的科里化:
>>> make_adder(2)(3)
5
>>> add(2,3)
5如何进行函数的科里化呢?
def curry2(f):
"""
f is a function with 2 arguments.
"""
def g(x):
def h(y):
return f(x,y)
return h
return g这样的话:
make_adder = curry2(add)
# make_adder(2)(3)就等价于add(2,3)
# curry2(add)返回的是g,且”记住了“add
# curry2(add)(2)返回的是h,且”记住了“add、x=2
# curry2(add)(2)(3)返回的是f(x,y) <<< ”记住了“add、x=2,还要传入的y=34.5 「Application 2」Lambda Expressions
什么是lambda函数?与def statements的区别?什么时候用它更好?
- lambda expression evaluates to a function.
- 如:
square = lambda x: x * x——squareis a function!
Lambda expressions VS Def statements
- 一样的domain、range、behavior
- 一样的parent frame——当他们defined时所在的frame
- 只有def statement会给function一个「intrinsic name」(下图中红色框的部分)
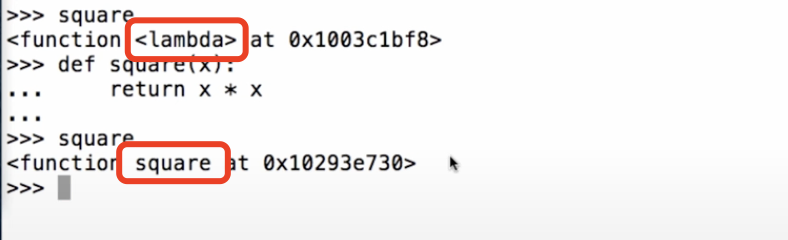

4.6 「Application 3」Decorators
本质是一个高阶函数;吃一个函数,吐出该函数的另一个版本——装饰版本
下图中@trace1中的trace1本质上是一个高阶函数:
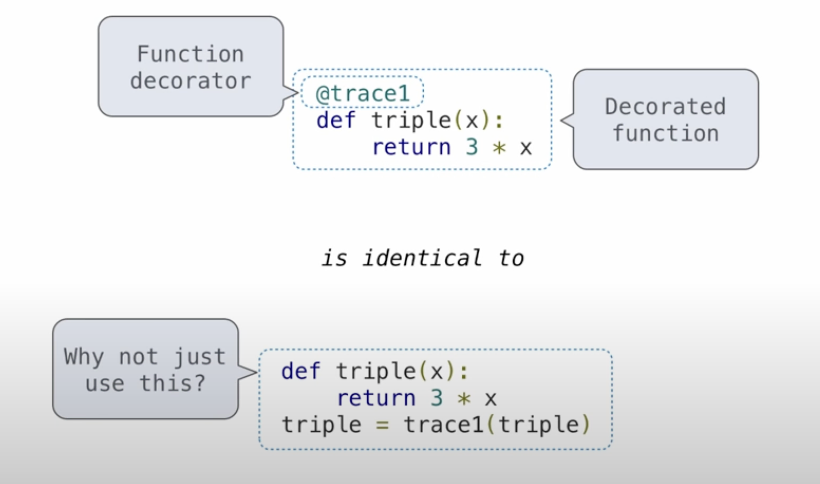
【例题】Natural Chain:利用higher-order function记忆状态的经典案例。
5. Recursion
5.1 Recursion Functions
Def(Recursive function): A function is called recursive if the body of that function calls itself, either directly or indirectly.
递归函数的「套路/模式」:
- 函数体一开始有一个conditional statement,用于检查base cases——very very simple versions of the problem that can be solved without recursive calls.
- 其余部分是recursive case——evaluated with recursive calls.
基于上述「套路/模式」,检查一个递归函数是否正确的流程(以递归求阶乘函数fact为例):
- Verify the base case.
- Treat
factas a functional abstraction. - Assume that
fact(n-1)is correct. - Verify that
fact(n)is correct, assuming thatfact(n-1)correct.
5.2 Mutual Recursion
Two functions call each other.
Example: Is Even and Is Odd
- A number is even if it’s one more than an odd number.
- A number is odd if it’s one more than an even number.
- 0 is a even number.
def is_even(n):
if n == 0:
return True
return is_odd(n-1)
def is_odd(n):
if n == 0:
return False
return is_even(n-1)【附】上述例子的讲解视频:CS 61A Departmental
5.3 Tree Recursion
Def (tree recursion): Tree-shaped processes arise whenever executing the body of a recursive function makes more than one call to that function.
Example: Fibonacci Numbers
def fib(n):
if n==0:
return 0
elif n==1:
return 1
else:
return fib(n-2) + fib(n-1)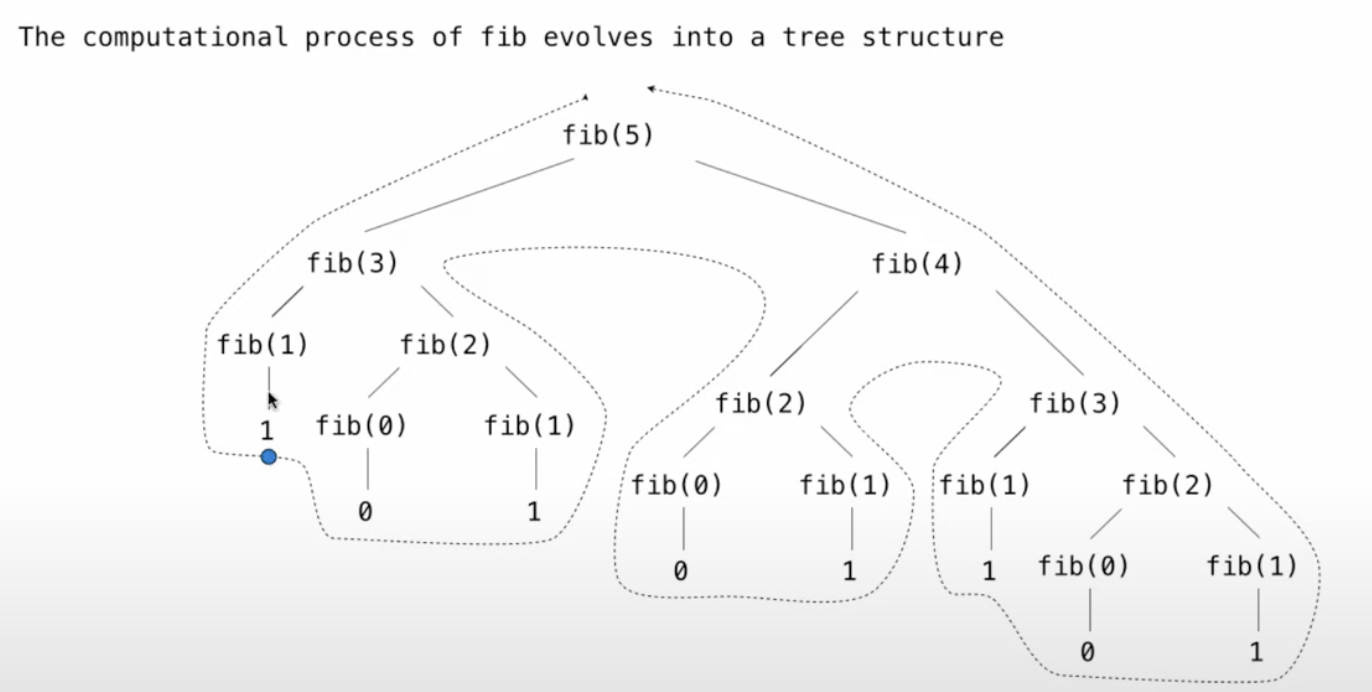
- 蓝色点:在计算fib(5)过程中第一个到达的return value
- 发现:重复计算
- 计算
fib(35)很慢了! - 可以使用
@trace来看 - 加速:记忆(例如通过字典,因为字典查找是O(1))
- 计算
5.4 Example: Counting Partitions
Function description: Count the ways to partition n using parts up to m.
- input: n和m
- n表示要被partition的数字
- m表示partition中最大的那个数字
- output:
count_partitions(n,m)- 返回partition的数量。一个例子(分解数字6,组分中最大值不超过4) ↓↓↓
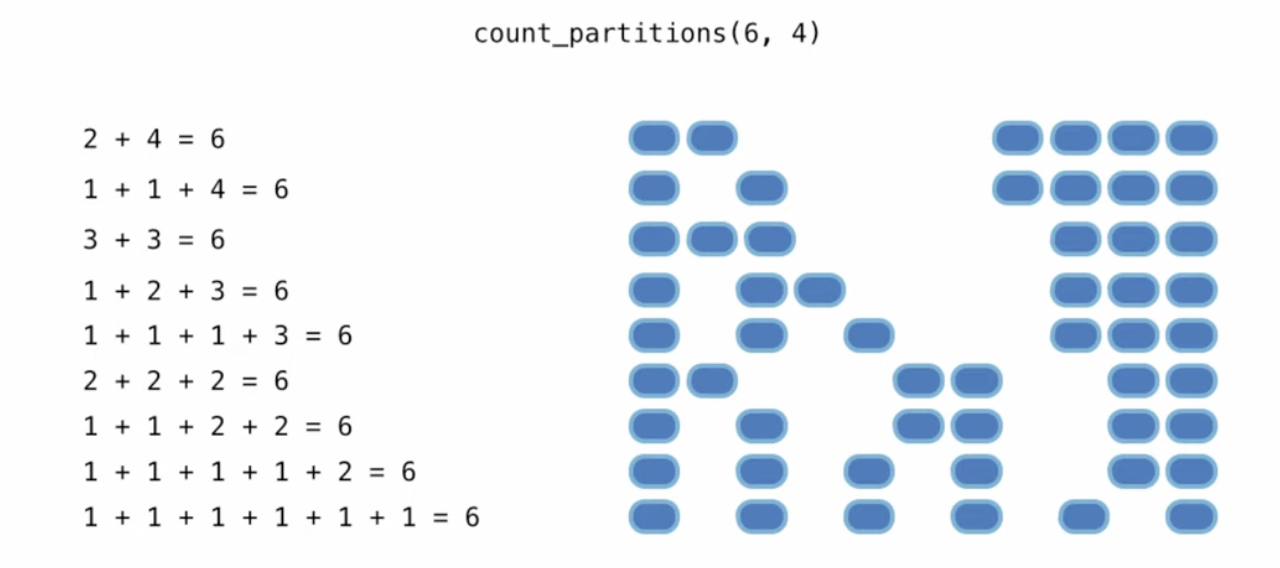
首先容易想到递推关系:
- 所有分割方法可以划分为互斥的两类
- ①至少使用一个m的:count_partitions(n-m, m)
- ②一个m都没有使用的:count_partitions(n, m-1)
- 因此有:count_partitions(n, m) = count_partitions(n-m, m) + count_partitions(n, m-1)
其次再想base cases
- n == 0 >>> There is one way to partition 0: include no parts >>> return 1
- n < 0 >>> return 0
- m == 0 >>> return 0
def count_partitions(n, m):
"""Count the ways to partition n using parts up to m."""
if n == 0:
return 1
elif n < 0:
return 0
elif m == 0:
return 0
else:
return count_partitions(n-m, m) + count_partitions(n, m-1)