NumPy是一个开源的Python科学计算基础库:
- 提供了一个强大的N维数组对象ndarray——numpy中几乎所有的操作均基于ndarray;
- 广播功能函数;
- 整合C/C++代码的工具;
- 线性代数、傅里叶变换、随机数生成等功能;
- NumPy是SciPy、Pandas等数据处理或科学计算库的基础。
NumPy库的标准导入方法(使用别名):
import numpy as np注意,本文自此以后将「ndarray数组」简称为「数组」。
Table of contents
1. 什么是数组 (ndarray)
1.1 概念
数组 vs 列表:
- 相似:都是表示一组数据的有序结构;
- 区别:列表中数据类型可以不同,数组则要求数据类型相同。
数据类型相同:
- 数组可以由非同质对象构成,但是非同质数组无法有效发挥NumPy的优势,所以尽量避免使用;
- 对元素类型精细定义,有助于NumPy合理使用存储空间并优化性能 + 程序员对程序规模合理评估。
重要概念:
- 维度(dimension):和数学里面的维度有所区别——
[1,2,3]是1维而不是3维,[[1,2,3],[4,5,6]]是2维而不是3维。可以查看数组对象的shape属性; - 轴(axis):一个维度对应一个轴,轴的编号从0开始,第0轴表示最外层维度,第1轴向里进一层;
- 秩(rank):即轴的数量/维度,
[[1,0,0],[0,0,0],[0,0,0]]秩是2而不是1; - sum部分更加具体介绍,暂记二维:对axis=0操作即对列操作,对axis=1操作即对行操作。
1.2 属性
arr = np.array([[1,2,3],
[4,5,6]])# 数组的维度,int
arr.ndim2# 数组的形状(每个维度的大小,从第0轴开始)
# 一般是一个tuple
arr.shape(2, 3)# 数组的总大小,shape中元素相乘
arr.size6# 数组元素的类型
arr.dtypedtype('int64')# 每个数组元素的字节大小
arr.itemsize81.3 数据类型
- 数组包含同一类型的值,即元素类型必须相同;
- 构建数组时,使用关键字参数
dtype来指定数据类型。可以使用字符串来指定,如dtype='int16',也可以用对象来指定dtype=np.int16。
常用:
bool:布尔值int32:整型,范围从-2^31到-2^31-1float32:单精度浮点数float64:双精度浮点数
np.array([True, False, True]).dtypedtype('bool')2. 数组的创建
2.1 从无到有
# 全零数组
np.zeros((2,3))array([[0., 0., 0.],
[0., 0., 0.]])# 全1数组
np.ones((3,3))array([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])# 全指定值数组
np.full((2,3), 10)array([[10, 10, 10],
[10, 10, 10]])# 单位矩阵
np.eye(4)array([[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]])# 创建一个线性序列数组,一般常跟reshape配合生成多维数组
np.arange(10)array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])# 接受起始点、结束点、节点数量三个参数,均匀分配
np.linspace(0,5,6)array([0., 1., 2., 3., 4., 5.])2.2 从已有数据构建
# 从list
np.array([1,2,3])array([1, 2, 3])# 从tuple
np.array((1,2,3))array([1, 2, 3])# 使用dtype参数指定数组元素的类型
np.array([1,2,3], dtype='float32')array([1., 2., 3.], dtype=float32)# dtype可以是字符串,也可以是np的对象
np.array([1,2,3], dtype=np.float32)array([1., 2., 3.], dtype=float32)# 嵌套
np.array([[1,2,3],[4,5,6]])array([[1, 2, 3],
[4, 5, 6]])# 复杂一点的例子,配合了列表解析
np.array([range(i,i+3) for i in [2,4,6]])array([[2, 3, 4],
[4, 5, 6],
[6, 7, 8]])# np.ones_like(a)
# 根据数组(序列)a的形状形成一个全1数组
x = [[1,2,3],[4,5,6]]
np.ones_like(x)array([[1, 1, 1],
[1, 1, 1]])# np.zeros_like(a)
# 根据数组(序列)a的形状形成一个全1数组
np.zeros_like(x)array([[0, 0, 0],
[0, 0, 0]])# np.full_like(a, val)
# 根据数组(序列)a的形状形成一个全val数组
np.full_like(x,111)array([[111, 111, 111],
[111, 111, 111]])2.3 随机数函数
1) 简单随机数函数
# 设定随机数种子——伪随机的概念,数序
np.random.seed(0)# np.random.random((d0,d1,...,dn))
# 返回一个或一组服从“0~1均匀分布”(包括0但不包括1)的随机样本值
np.random.random((2,3))array([[0.5488135 , 0.71518937, 0.60276338],
[0.54488318, 0.4236548 , 0.64589411]])# np.random.rand(d0,d1,...,dn)
# 作用与np.random.random相同
# If you want an interface that takes a shape-tuple as the first argument
# refer to np.random.random
np.random.rand(2,3)array([[0.56804456, 0.92559664, 0.07103606],
[0.0871293 , 0.0202184 , 0.83261985]])# np.random.randn(d0,d1,...dn)
# 根据形状创建随机数数组,浮点数,标准正态分布
np.random.randn(2,3)array([[ 0.44386323, 0.33367433, 1.49407907],
[-0.20515826, 0.3130677 , -0.85409574]])# np.random.randint(low[,high,shape])
# 根据shape创建整数或整数数组,范围是[low,high)
# “If high is None (the default), then results are from [0,low)”
np.random.randint(0,100,(2,3))array([[ 9, 57, 32],
[31, 74, 23]])2) 高级随机数函数
# np.random.uniform(low, high, size)
# 产生具有均匀分布的数据
# low起始值,high结束值,size形状,[low,high)
np.random.uniform(0,100,(3,4))array([[69.76311959, 6.02254716, 66.67667154, 67.06378696],
[21.03825611, 12.89262977, 31.54283509, 36.37107709],
[57.01967704, 43.86015135, 98.83738381, 10.20448107]])# np.random.normal(loc, scale, size)
# 产生具有正态分布的数据,loc均值,scale标准差,size形状
np.random.normal(5,2,(2,3))array([[3.98069564, 4.1238514 , 2.49440928],
[6.55498071, 1.7722043 , 4.57451944]])# np.random.poisson(lam, size)
# 产生具有泊松分布的数据,lam随机事件发生率,size形状
np.random.poisson(2,(2,3))array([[1, 1, 1],
[1, 1, 5]])3) 随机重排
# np.random.shuffle(a)
# 只接受一个参数
# 根据数组a的第0轴进行随机排列,改变数组a
a = np.arange(10)
np.random.shuffle(a)
aarray([0, 5, 7, 8, 1, 4, 9, 6, 2, 3])# np.random.permutation(a)
# 同上,但不改变数组a
c = np.arange(10)
np.random.permutation(c)array([1, 4, 7, 5, 2, 3, 8, 6, 9, 0])carray([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])# np.random.choice(a, [,size, replace, p])
# 从1维数组a中以概率p抽取元素,形成size形状的新数组
# replace表示是否可以重用元素,默认为Ture
d = np.random.randint(100,201,(8,))
darray([140, 172, 119, 195, 172, 126, 166, 152])np.random.choice(d, (2,3))array([[195, 126, 195],
[172, 166, 126]])np.random.choice(d, (2,3), replace=False)array([[119, 195, 152],
[172, 140, 172]])np.random.choice(d, (2,3), p=d/np.sum(d))array([[126, 119, 195],
[166, 152, 140]])3. 数组的变形
3.1 reshape
.reshape(),常用于将一维数组扩展为多维数组:
np.arange(10).reshape(2,5)array([[0, 1, 2, 3, 4],
[5, 6, 7, 8, 9]])3.2 resize
.resize(),效果和reshape一样,但修改原数组——reshape是返回一个新的数组而原数组不变。
a = np.arange(10)
a.resize(2,5)
aarray([[0, 1, 2, 3, 4],
[5, 6, 7, 8, 9]])a = np.arange(10)
a.reshape(2,5)
aarray([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])3.3 newaxis
将一个一维数组,转变成为二维的行或列的矩阵(完全可以用reshape来做):
x = np.array([1,2,3])
xarray([1, 2, 3])# 行矩阵 = x.reshape(1,3)
x[np.newaxis, :]array([[1, 2, 3]])# 列矩阵 = x.reshape(3,1)
x[:, np.newaxis]array([[1],
[2],
[3]])3.4 flatten
.flatten(),对数组进行降维,返回折叠后的一维数组,原数组不变。
a = np.array([[1,2,3],
[4,5,6],
[7,8,9]])
a.flatten()array([1, 2, 3, 4, 5, 6, 7, 8, 9])aarray([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])3.5 astype
.astype(),对数组元素进行类型变换,注意astype方法一定会创建新的数组,即使两个类型一样。
# new_a = a.astype(new_type)
a = np.ones((2,2), dtype="int32")
aarray([[1, 1],
[1, 1]], dtype=int32)a.astype("float32")array([1.9, 1.9, 1.9, 2.8], dtype=float32)4. 索引与切片
4.1 普通索引
支持正向索引与反向索引:
a = np.arange(10)
aarray([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])a[1]1a[-2]8多维数组可以用一个中括号辅以「逗号」来获取深层元素,如a[0,0]和普通list的a[0][0]等价。
b = np.arange(12).reshape(3,4)
barray([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])# 第2行第2列元素
b[1,1]5可以使用索引直接修改数组。注意,试图将一个浮点数插入到一个整型数组中,会发生无任何警告的截断操作(不是四舍五入)。
b[-1,-1]11b[-1,-1] = 199.9999999
barray([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 199]])4.2 花式索引
fancy indexing,传递一个索引数组来一次性获得多个数组元素。
x = np.array([1,2,3,4,5,6,7])
ind = [0,1,2,3]
x[ind]array([1, 2, 3, 4])多维数组的花式索引:
X = np.arange(24).reshape((4,6))
Xarray([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17],
[18, 19, 20, 21, 22, 23]])# 第一个值是X[1,2],第二个值是X[3,4]
row = np.array([1,3])
col = np.array([2,4])
X[row, col]array([ 8, 22])# 交换任意两行
A = np.arange(25).reshape(5,5)
Aarray([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19],
[20, 21, 22, 23, 24]])# A[[0,1]] 等价于 A[[0,1],] 等价于 A[[0,1],:],表示前两行
A[[0,1]] = A[[1,0]]
Aarray([[ 5, 6, 7, 8, 9],
[ 0, 1, 2, 3, 4],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19],
[20, 21, 22, 23, 24]])4.3 切片
索引获取单个值,切片获取子数组。语法为x[start:stop:step],默认值分别为start=0, stop=size of dimension, step=1。step为负的时候表示逆向截取。
a = np.arange(10)
aarray([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])a[1:7]array([1, 2, 3, 4, 5, 6])a[::-1]array([9, 8, 7, 6, 5, 4, 3, 2, 1, 0])多维数组的切片不同维度用逗号分隔进行操作。对于二维数组x,x[:2, :3]表示切到前两行+前三列。
b = np.arange(12).reshape(3,4)
barray([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])b[:2,:2]array([[0, 1],
[4, 5]])获取数组的单行或单列:将切片和索引配合使用。
# 单行
b[1,:]array([4, 5, 6, 7])# 单列
b[:,1]array([1, 5, 9])关于副本(copy)和视图(view):切片切出来的是view而非copy,故对切片的修改会影响到原数组。
barray([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])temp = b[0,:]
temparray([0, 1, 2, 3])temp[1] = 100
temparray([ 0, 100, 2, 3])barray([[ 0, 100, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])目的:这样做可以节省缓存空间。可以使用切片.copy()获得副本;对副本操作,不会影响原数组。
5. 拼接与分裂
5.1 拼接
将多个数组拼接成一个。
1) concatenate
np.concatenate(),默认按照第0轴拼接,可以一次性拼接多个,但要把拼接的数组先以列表或元组的形式圈起来,如np.concatenate([x,y,z])。
a1 = np.arange(6).reshape(2,3)
a1array([[0, 1, 2],
[3, 4, 5]])addarr = np.array([6,7,8])
addarrarray([6, 7, 8])add1 = addarr[np.newaxis, :]
np.concatenate([a1, add1])array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])对于多维数组的拼接,np.concatenate([x,y], axix=指定轴)。
add2 = addarr[:-1, np.newaxis]
np.concatenate([a1, add2], axis=1)array([[0, 1, 2, 6],
[3, 4, 5, 7]])2) vstack & hstack
a1array([[0, 1, 2],
[3, 4, 5]])np.vstack: 垂直栈。垂直方向对接,同样要把拼接的数组先以列表或元组的形式圈起来,但拼上去的一维数组不需要先转成2维再拼接,可以直接拼接。
np.vstack([a1,a1])array([[0, 1, 2],
[3, 4, 5],
[0, 1, 2],
[3, 4, 5]])np.vstack([a1,a1[0]])array([[0, 1, 2],
[3, 4, 5],
[0, 1, 2]])# 并不需要
np.vstack([a1,a1[0][np.newaxis,:]])array([[0, 1, 2],
[3, 4, 5],
[0, 1, 2]])np.hstack:水平栈。水平方向拼接,同样要把拼接的数组先以列表或元组的形式圈起来。
np.hstack([a1,a1])array([[0, 1, 2, 0, 1, 2],
[3, 4, 5, 3, 4, 5]])np.hstack([a1,a1[:,1][:,np.newaxis]])array([[0, 1, 2, 1],
[3, 4, 5, 4]])5.2 分裂(略)
np.split(x, [...]):第一个参数是要进行分裂的数组,第二个参数是一个索引列表,记录分裂点。
x = [1,2,3,99,99,3,2,1]
x1,x2,x3 = np.split(x, [3,5])
print(x1,x2,x3)[1 2 3] [99 99] [3 2 1]np.vsplit(): 垂直栈,分开。
grid = np.arange(16).reshape(4,4)
gridarray([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15]])upper, lower = np.vsplit(grid, [2])
print(upper)
print(lower)[[0 1 2 3]
[4 5 6 7]]
[[ 8 9 10 11]
[12 13 14 15]]np.hsplit():水平栈,分开。
left, right = np.hsplit(grid, [2])
print(left)
print(right)[[ 0 1]
[ 4 5]
[ 8 9]
[12 13]]
[[ 2 3]
[ 6 7]
[10 11]
[14 15]]6. 广播
广播的实质:用于不同大小数组的二元通用函数的一组规则——Broadcasting allows computation to be performed on arrays of different sizes.
a = 5
b = np.array([1,2,3])
a+barray([6, 7, 8])相当于把5扩展成array([5,5,5]),然后再相加。但是Numpy的强大之处在于,并没有显性地执行这种duplication,节省了很多空间。
c = np.array([[1,1,1],
[2,2,2],
[3,3,3]])
b+carray([[2, 3, 4],
[3, 4, 5],
[4, 5, 6]])相当于把[1,2,3]扩展成[[1,2,3],[1,2,3],[1,2,3]],然后再相加。
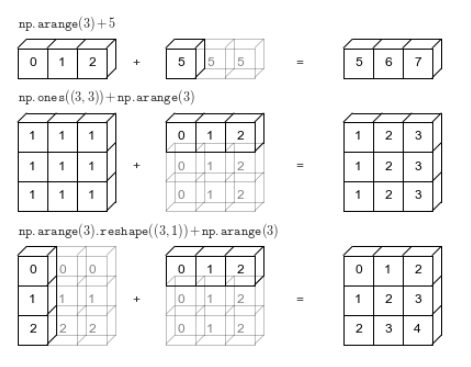
广播规则:
- Rule 1: If the two arrays differ in their number of dimensions, the shape of the one with fewer dimensions is padded with ones on its leading (left) side.
- 如果两个数组的维度数量不相同,那么小维度数组的形状将会在最左边补1;
- Rule 2: If the shape of the two arrays does not match in any dimension, the array with shape equal to 1 in that dimension is stretched to match the other shape.
- 维度数量相同后,数组的形状会沿着维度为1的扩展以匹配另外一个数组的形状;
- Rule 3: If in any dimension the sizes disagree and neither is equal to 1, an error is raised.
- 如果维度数量相同,但都不匹配且没有为1的,异常。
失败案例:
M = np.ones((3, 2))
a = np.arange(3)形状:
- M.shape = (3, 2)
- a.shape = (3,)
根据Rule 1:
- M.shape = (3, 2)
- a.shape = (1, 3)
根据Rule 2:
- M.shape = (3, 2)
- a.shape = (3, 3)
根据Rule 3:
- 失败
X = np.arange(24).reshape((4,6))
row = np.array([1,3])
col = np.array([2,4])
X[row, col]array([ 8, 22])# 广播,十分有用,交叉点元素
# row[:, np.newaxis] - 列向量1,3
# col - 行向量2,4
X[row[:, np.newaxis], col]array([[ 8, 10],
[20, 22]])8. 函数
8.1 通用函数
1) 算术运算
原生的算术运算符,实质上是NumPy通用函数的封装器,例如+就是np.add的封装器。
x = np.zeros(5)
xarray([0., 0., 0., 0., 0.])x+2array([2., 2., 2., 2., 2.])np.add(x,2)array([2., 2., 2., 2., 2.])| 运算符 | 对应的通用函数 | 描述 |
| + | np.add | 加法 |
| - | np.subtract | 减法 |
| * | np.multiply | 乘法 |
| / | np.divide | 除法 |
| // | np.floor_divide | 向下整除 |
| ** | np.power | 指数 |
| % | np.mod | 取余 |
2) 其他
- 绝对值:
np.abs - 三角函数:
np.sin,np.cos,np.tan - 指数函数:
np.exp(底数是e),np.exp2(底数是2) - 对数:
np.log(底数是e),np.log2(底数是2),np.log10(底数是10) np.power(x,n):x的n次方np.sqrt(x):平方根np.rint(x):各元素四舍五入np.modf(x):将数组中各元素的小数和整数部分以两个独立的数组形式返回np.sign(x):计算数组各元素的符号值,1(+),0,-1(-)
8.2 聚合函数
最常用的三种:
- np.sum
- np.min
- np.max
轴的再理解:参考资料
a = np.array([[[1,2,3],
[1,2,3],
[1,2,3]],
[[4,5,6],
[4,5,6],
[4,5,6]]])
aarray([[[1, 2, 3],
[1, 2, 3],
[1, 2, 3]],
[[4, 5, 6],
[4, 5, 6],
[4, 5, 6]]])np.sum(a)63a.shape(2, 3, 3)# keepdims,保留维度信息
np.sum(a, axis=0, keepdims=True)array([[[5, 7, 9],
[5, 7, 9],
[5, 7, 9]]])np.sum(a, axis=1, keepdims=True)array([[[ 3, 6, 9]],
[[12, 15, 18]]])np.sum(a, axis=2, keepdims=True)array([[[ 6],
[ 6],
[ 6]],
[[15],
[15],
[15]]])理解:axis指定的是数组将会被折叠的维度。
大多数聚合函数都应版本的NaN-safe函数,即计算时忽略所有的缺失值,只需在名字前面加nan。例如,np.sum的缺失值安全版本是np.nansum。
其他常用聚合函数:
- np.prod:计算元素的积
- np.mean:平均值
- np.std:标准差
- np.var:方差
- np.argmin:最小值的索引
- np.argmax:最大值的索引
- np.median:中位数
- np.percentile:计算基于元素排序的统计值
- np.any:验证是否存在元素为真
- np.all:验证所有元素是否为真
9. 比较与逻辑
场景:希望基于某些准则来抽取、修改、计数或对一个数组中的值进行其他操作。
9.1 比较运算与布尔数组
比较运算符与对应的通用函数(返回布尔数据类型的数组):
==, np.equal!=, np.not_equal<, np.less<=, np.less_equal>, np.greater>=, np.greater_equal
# x==3就返回一个布尔数组
x = np.array([1,2,3,4,5])
x == 3array([False, False, True, False, False])对布尔数组的常用操作:
np.count_nonzero():统计True的个数np.sum():统计True的个数,能够按轴统计np.any():是否有Truenp.all():是否全是True
np.count_nonzero(x==3)1np.any(x==3)Truenp.all(x==3)False9.2 掩码
使用布尔数组作为掩码(mask),通过该掩码选择数据的子数据集:
xarray([1, 2, 3, 4, 5])# 抽取x中大于3的元素
x[x>3]array([4, 5])y = np.arange(12).reshape(3,4)
yarray([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])# 抽取y中大于等于7的元素,展开
y[y>=7]array([ 7, 8, 9, 10, 11])9.3 逐位运算符
逐位布尔运算符:
&, np.bitwise_and|, np.bitwise_or^, np.bitwise_xor-, np.bitwise_not
and和or对整个对象执行单个布尔操作,而&和|对一个对象的内容执行多个布尔运算,下例:
a = np.array([True, False, True])
b = np.array([True, True, False])# 对a和b中每一对对应的元素进行“逻辑与”的运算
a & barray([ True, False, False])# 对a和b中每一对对应的元素进行“逻辑或”的运算
a | barray([ True, True, True])10. 其他重要方法
10.1 np.meshgrid
生成网格点坐标矩阵(类似双列表解析):
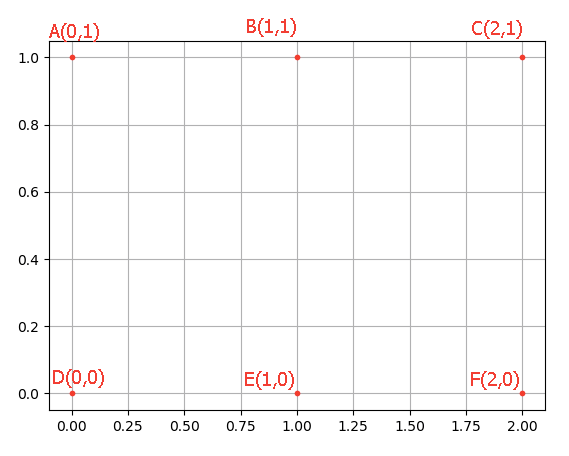
x = [1,2,3]
y = [1,2]
np.meshgrid(x,y)
# [(i,j) for i in x for j in y][array([[1, 2, 3],
[1, 2, 3]]), array([[1, 1, 1],
[2, 2, 2]])]用途:绘制等高线图。
10.2 np.where
np.where(condition, x, y):满足条件,返回x,否则返回y。
aa = np.array([[1,2],
[3,4],
[5,6]])
np.where(aa>=3, 1, -1)array([[-1, -1],
[ 1, 1],
[ 1, 1]])np.where(condition):找到数组中特定数值的索引:
bb = np.array([[1,2,3],
[3,4,5]])
np.where(bb>=3)(array([0, 1, 1, 1]), array([2, 0, 1, 2]))10.3 np.sort
一维数组排序(重新创建而非就地修改):
np.random.seed(0)
a = np.random.randint(0,20,(10))
aarray([12, 15, 0, 3, 3, 7, 9, 19, 18, 4])# 默认升序
np.sort(a)array([ 0, 3, 3, 4, 7, 9, 12, 15, 18, 19])# 数组排好序的索引值
np.argsort(a)array([2, 3, 4, 9, 5, 6, 0, 1, 8, 7])多维数组排序,用axis=指定排序的轴,注意这样排序会导致任何行或列之间的关系丢失!
np.random.seed(1)
X = np.random.randint(0,100,(4,5))
Xarray([[37, 12, 72, 9, 75],
[ 5, 79, 64, 16, 1],
[76, 71, 6, 25, 50],
[20, 18, 84, 11, 28]])np.sort(X, axis=0)array([[ 5, 12, 6, 9, 1],
[20, 18, 64, 11, 28],
[37, 71, 72, 16, 50],
[76, 79, 84, 25, 75]])np.sort(X, axis=1)array([[ 9, 12, 37, 72, 75],
[ 1, 5, 16, 64, 79],
[ 6, 25, 50, 71, 76],
[11, 18, 20, 28, 84]])10.4 np.insert
给矩阵插入行或列。
a = np.array([[1,0,2,3],
[1,0,2,3],
[1,0,2,3]])
aarray([[1, 0, 2, 3],
[1, 0, 2, 3],
[1, 0, 2, 3]])np.insert(a, 1, values = np.ones((2,a.shape[1])), axis = 0)array([[1, 0, 2, 3],
[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 0, 2, 3],
[1, 0, 2, 3]])