Table of contents
- Entity Fixed Effects = Control For Entity
- Illustration
- Two-way Fixed Effects
- Random Effects
- Reference
Entity Fixed Effects = Control For Entity
Fixed effects is a method of controlling for all variables, whether they’re observed or not, as long as they stay constant within some larger category… we’re controlling for a variable higher up on the hierarchy of our hierarchical data.
Suppose “individual” is the higher level (e.g., one individual has multiple observations over time). In this case, “individual” or “entity” fixed effects control for between-individual variation, that is to say, removing any variation between individuals. Hence, only variation within individuals remains >>> Therefore, we can purely examine the relationship between the variation in X and the variation in Y within individuals.
Another view: If we suspect the presence of observable or unobservable confounders that remain constant within individuals, we can control for these individuals directly, ensuring that all such within-constant & between-variable things are controlled for - In this way, the variation among DV cannot be attributed to these controlled factors.
Illustration
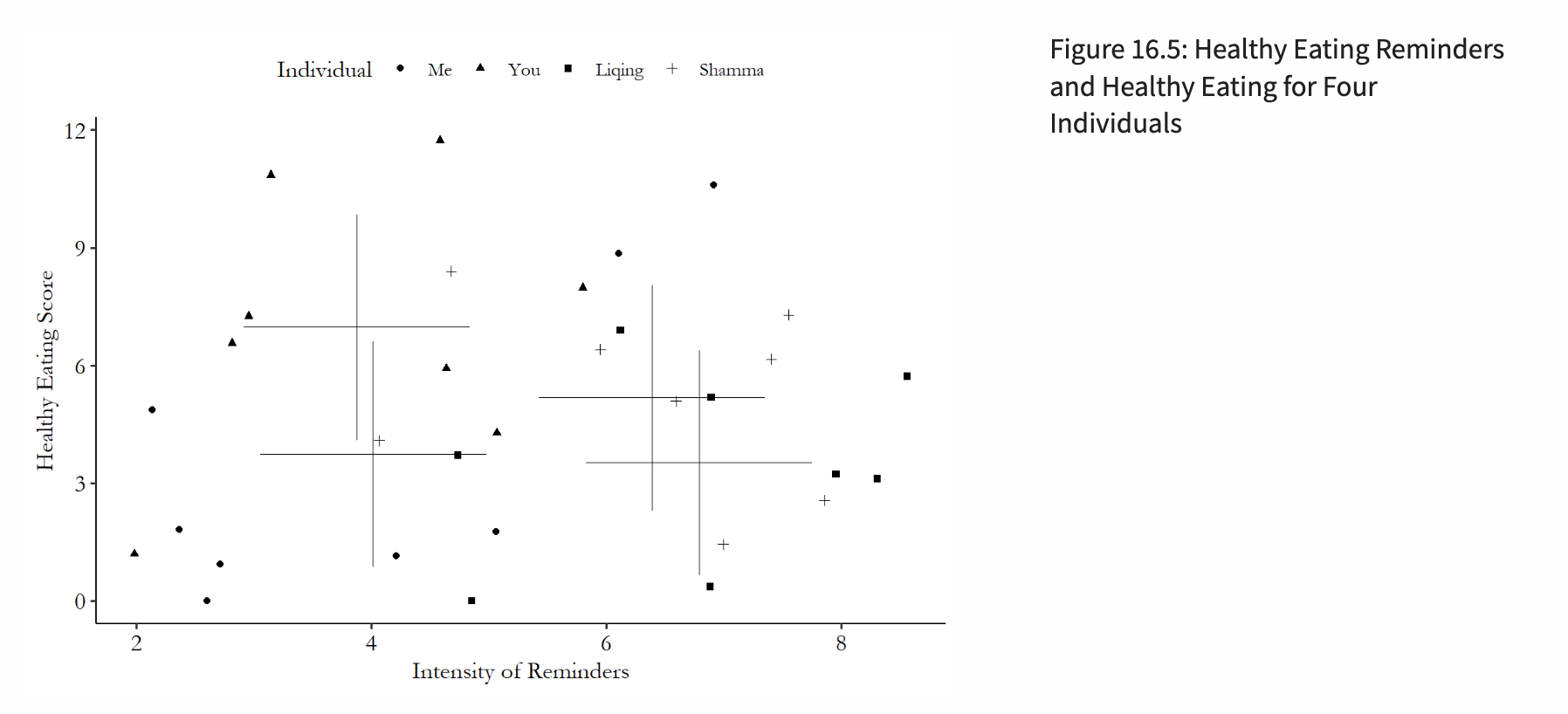
- Overall - negative relationshio (-.440)
- Four crosses refer to four pairs of means, each corresponding to an individual.
- Four crosses = between-individual variation
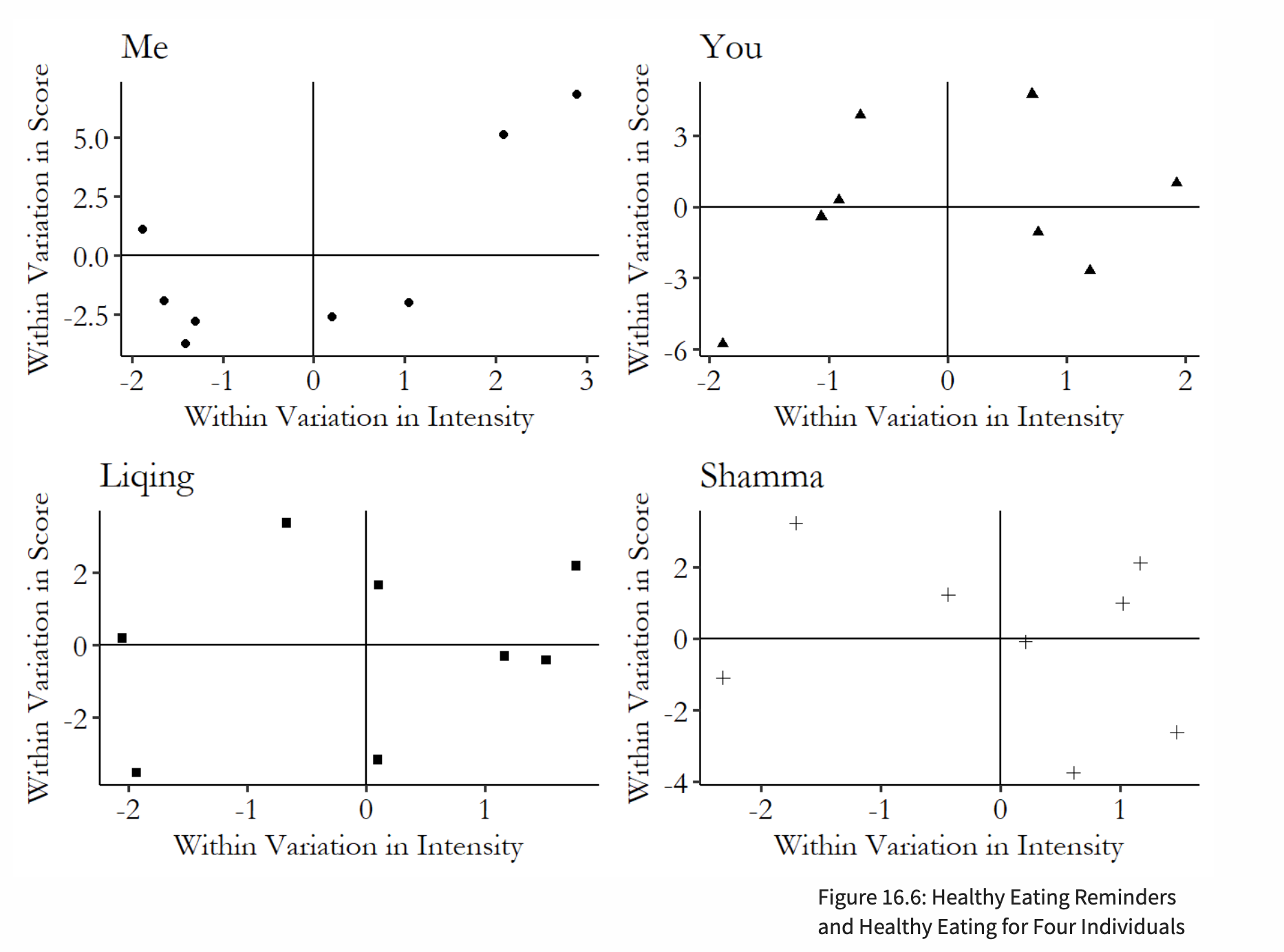
- Each graph refers to within-individual variation.
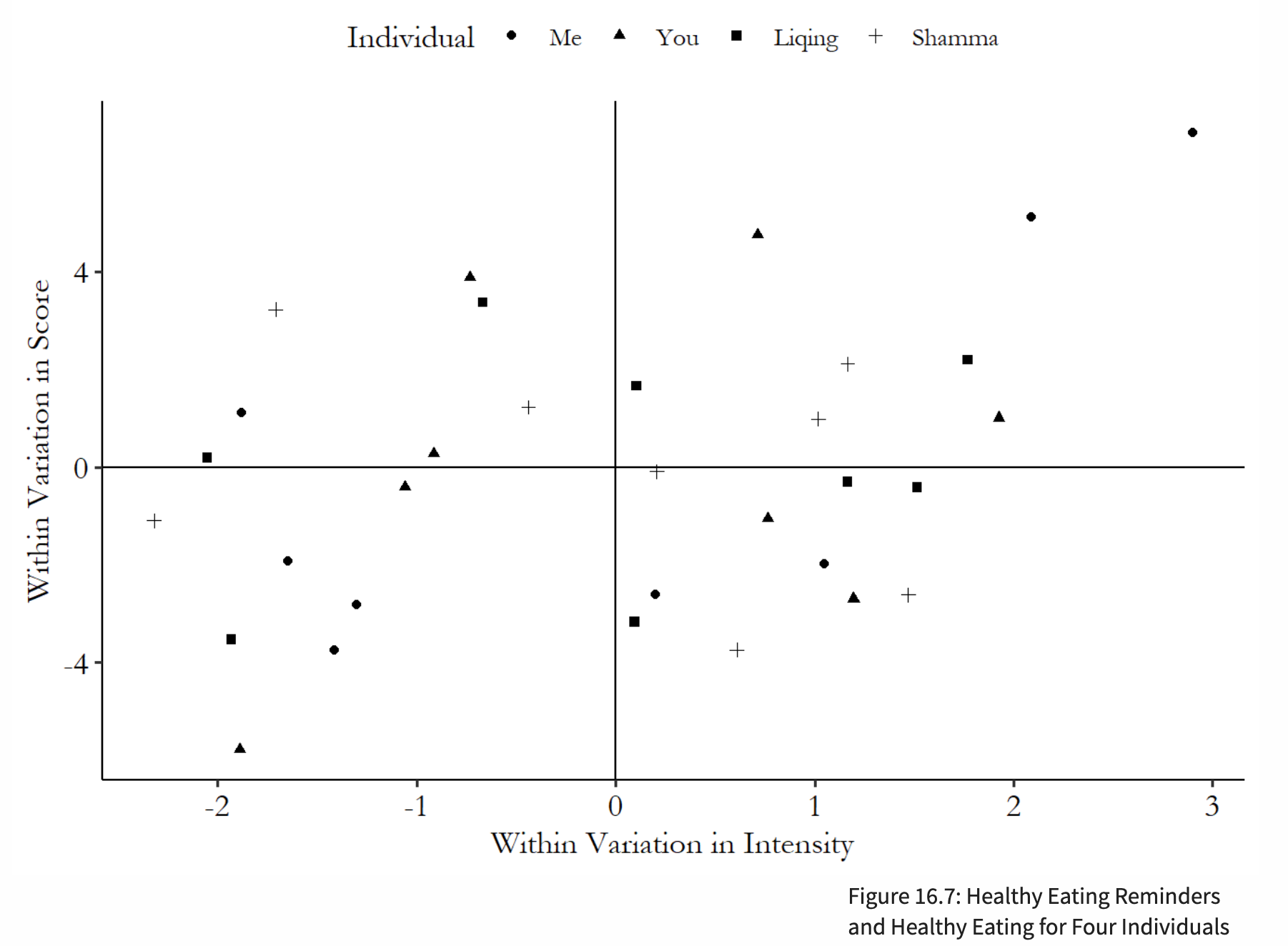
- Overlay the four crosses >>> Get rid of between-individual variation
- Within variation of X ~ within variation of Y
These diagrams illustrate the estimation method corresponding to the Within Estimator, which involves applying mean centering to the data points. Another diagram demonstrates fitting a separate line for each individual’s data points, but with the same slope for all individuals—this corresponds to the LSDV estimation method.
- The template for interpreting the fixed effects model’s results: “For a given xxx (level you fixed), one change in X related to xxx change in Y.”
Two-way Fixed Effects
Fixed effects = control for dummies = focus on the variation within that variable:
- If we have fixed effects for individual, we are comparing that individual to themselves over time (index=it, i means individual and t means time).
- If we have fixed effects for city, we are comparing units in that city only to other units in that city (index=ij, i means unit and j means city).
Add one fixed effect = remove between-that-variable variation = focus on within-that-variable variation of X and Y. We can add two fixed effects at the same time:
- If we have fixed effects for individual, we are comparing that individual to themselves over time.
- If we have fixed effects for year, we are comparing individuals to each other at the same period of time.
- If we have both fixed effects, we are looking at variation within individual as well as within year - “variation relative to what we’d expect given that individual, and given that year”.
We can have two sets of fixed effects and neither of them is time:
- For example, you could have fixed effects for individual and also for city.
- Twins: Since twins have the same parents, were mostly raised together, and may even have the same genes, we might reasonably assume their ability, motivation, talent, … are the same, if they are the twins in the same family >>> In this case, two children in one family ≈ one person observed twice.
Random Effects
- The fixed effects model focuses on isolating within-XXX variation because between-XXX variation may introduce backdoor paths, which we need to eliminate.
- Fixed effects are designed to address issues in research design (i.e., unobservable confounders), while random effects are not. We can use the random effects model only if we assume there are no unobservable confounders correlated with the independent variables.
- The Durbin-Wu-Hausman test is a broad set of tests that compare the estimates from one model to another to see if they differ. If the estimates from the fixed effects and random effects models are not significantly different, we can use the random effects model.