Method | Understanding Instrumental Variable within Potential Outcome Framework

Table of contents

• Review: Instrumental Variable Analysis
• Principal Stratification
• ITT Effect Decomposition
• Reference

Review: Instrumental Variable Analysis

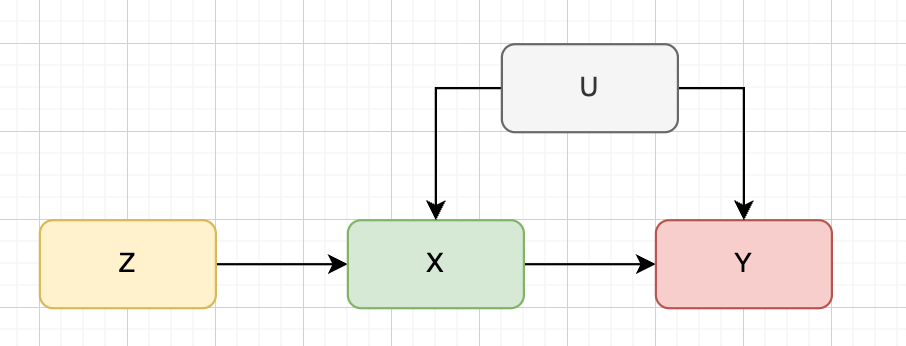
• Dilemma: We cannot directly regress Y on X because X is endogenous—there are unobservable confounders U related to both X and Y.
• Instrumental variable: We have a variable Z satisfying two conditions: ①instrumental exogeneity: Cov(Z,e)=0, meaning no confounders affect Z and Z affects Y only through X; ②instrumental relevance: Cov(Z,X)≠0.
• Identification: We have IV estimand β=Cov(Z,Y)/Cov(Z,X) and we can regress X on Z first, then regress Y on the fitted values X_hat (i.e., two-stage least squares).

Principal Stratification

Notations for each individual i:

• $Z_i \in \{0,1\}$ - 0 means not encouraged, 1 means encouraged—this is the instrumental var.
• $(T_{i0},T_{i1}) \in \{0,1\}$ - this are potential treatments; each individual has these two digits.
  • 0&1 in index refers to the realization of Z
• Each individual i also has two potential outcomes $(Y_{i0}, Y_{i1})$
  • 0&1 in index also refers to the realization of Z (not T!)
• Randomization of encouragement Z means $Y_{i0},Y_{i1},T_{i0},T_{i1} \perp Z_i$
• But always keep in mind that the treatment is not random: no $Y_{i0},Y_{i1} \perp T_i\ |\ Z_i=z$

Based on $T_{i0}$ and $T_{i1}$, individuals fall into four groups:

• Compliers: $T_{i0}=0, T_{i1}=1$
• Always-takers: $T_{i0}=1, T_{i1}=1$
• Never-takers: $T_{i0}=0, T_{i1}=0$
• Defiers: $T_{i0}=1, T_{i1}=0$

To summarize:

Remarks: We can only observe one potential treatment for each individual, so we cannot identify which group an individual belongs to. Next, we’ll see that the IV estimand equals to the LATE estimand—the average treatment effect among compliers.

ITT Effect Decomposition

Intention-to-treat analysis focuses on the effect of encouragement to treatment, rather than the treatment eventually received—that is, the effect of Z on Y. We have:

In this decomposition, g refers to the four groups. Clearly, ITT effects for always-takers and never-takers are 0 because they always/never take the treatment regardless of Z. We also assume there are no defiers. Hence, we get:

We know Z is exogenous (i.e., Z is independent of potential treatments and outcomes), so:

The ITT effect for compliers is actually the ATE for compliers because for compliers, Z is equivalent to T:

Finally, what’s the proportion of compliers? Because Z is exogenous/randomly assigned, the proportions of compliers, always-takers, and never-takers are the same for Z=1 and Z=0. Hence:

To sum up,

Two hints for the last step:

• $Cov(Y,Z) = E(YZ)-E(Y) \cdot E(Z)$
• Law of total expectation: $E(Y) = E_ZE(Y|Z)$

Thus, the IV estimand is essentially the average treatment effect for the compliers, named “local average treatment effect (LATE).”

Reference

• Noncompliance in Randomized Experiments (harvard.edu)
• Interpreting Did and IV Estimates: ATE, ATET, LATE, and All That (cornell.edu)